题目内容
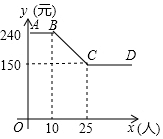
1.抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点,若直线y=-$\frac{1}{2}$x向上平移m个单位所得的直线与抛物线段BC段(包括端点B、C)部分有两个交点,则m的取值范围是$\frac{15}{8}$<m≤3.分析 根据点B、C的坐标利用待定系数法求出二次函数解析式,画出二次函数及一次函数图象,分别求出当直线经过点C及直线与抛物线相切时m的值,再结合图形即可得出结论.
解答 解:将B(-2,6)、C(2,2)代入y=ax2+bx+2,
$\left\{\begin{array}{l}{4a-2b+2=6}\\{4a+2b+2=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$,
∴二次函数解析式为y=$\frac{1}{2}$x2-x+2.
依照题意画出图形,如图所示.
当点C(2,2)在直线y=-$\frac{1}{2}$x+m上时,
2=-1+m,解得:m=3;
将y=-$\frac{1}{2}$x+m代入为y=$\frac{1}{2}$x2-x+2中,整理得:x2-x+4-2m=0,
当直线y=-$\frac{1}{2}$x+m与抛物线y=$\frac{1}{2}$x2-x+2相切时,有△=(-1)2-4×(4-2m)=0,
解得:m=$\frac{15}{8}$.
∴若直线y=-$\frac{1}{2}$x向上平移m个单位所得的直线与抛物线段BC段(包括端点B、C)部分有两个交点,则m的取值范围是$\frac{15}{8}$<m≤3.
故答案为:$\frac{15}{8}$<m≤3.
点评 本题考查了待定系数法求二次函数解析式、一次函数图象与几何变换、一次函数图象上点的坐标特征以及根的判别式,依照题意画出图形,利用数形结合解决问题是解题的关键.

练习册系列答案
相关题目
17.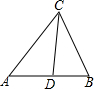 如图,CD是△ABC的角平分线,∠A=50°,∠B=60°,则∠ACD的度数是( )
如图,CD是△ABC的角平分线,∠A=50°,∠B=60°,则∠ACD的度数是( )
 如图,CD是△ABC的角平分线,∠A=50°,∠B=60°,则∠ACD的度数是( )
如图,CD是△ABC的角平分线,∠A=50°,∠B=60°,则∠ACD的度数是( )| A. | 35° | B. | 40° | C. | 145° | D. | 110° |
18.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (2ab2)2=4a2b4 | C. | (-a2)3=a6 | D. | 2a2÷a=2 |
6. 两个全等的正六边形如图摆放,与△ABC面积不同的一个三角形是( )
两个全等的正六边形如图摆放,与△ABC面积不同的一个三角形是( )
 两个全等的正六边形如图摆放,与△ABC面积不同的一个三角形是( )
两个全等的正六边形如图摆放,与△ABC面积不同的一个三角形是( )| A. | △ABD | B. | △ABE | C. | △ABF | D. | △ABG |
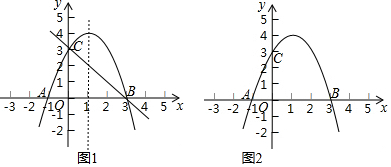
 某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.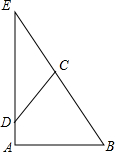 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.
如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.