题目内容
【课本节选】
反比例函数y= (k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y=(k>0)的增减性来进行说理.如图,当x>0时.
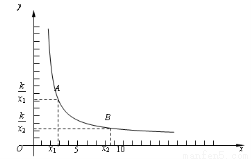
在函数图象上任意取两点A、B,设A(x1,),B(x2,),
且0<x1< x2.
下面只需要比较和的大小.
—= .
∵0<x1< x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴<0.即< .
这说明:x1< x2时,>.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.
同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y= (k>0)的图象关于原点对称.
【运用推广】
(2)分别写出二次函数y=ax2 (a>0,a为常数)的对称性和增减性,并进行说理.
对称性: ;
增减性: .
说理:
(3)对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),请你从增减性的角度,简要解释为何当x=— 时函数取得最小值.
练习册系列答案
相关题目


 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 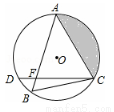
 与双曲线
与双曲线 的交点A的横坐标1,则关于x的不等式
的交点A的横坐标1,则关于x的不等式 的解集是( )
的解集是( )



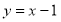 ,令
,令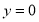 ,可得
,可得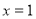 ,我们就说1是函数
,我们就说1是函数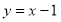 的零点.
的零点.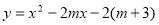 (
(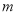 为常数).
为常数).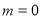 时,求该函数的零点;
时,求该函数的零点;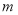 取何值,该函数总有两个零点.
取何值,该函数总有两个零点.