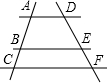
题目内容
如图，已知B是线段AE上一点，ABCD和BEFG都是正方形，连接AG、CE．
（1）求证：AG=CE；
（2）设CE与GF的交点为P，求证：
=
．
（1）求证：AG=CE；
（2）设CE与GF的交点为P，求证：
| PG |
| CG |
| PE |
| AG |
证明：（1）∵四边形ABCD和BEFG是正方形，
∴AB=CB，BG=BE，∠ABG=∠CBE=90°，
∴△ABG≌△CBE，
∴AG=CE，
（2）∵PG∥BE
∴
=
，
=
，
∵BG=BE，AG=CE，
∴
=
，
=
，
∴
=
．
∴AB=CB，BG=BE，∠ABG=∠CBE=90°，
∴△ABG≌△CBE，
∴AG=CE，
（2）∵PG∥BE
∴
| PG |
| BE |
| CG |
| CB |
| BG |
| CB |
| PE |
| CE |
∵BG=BE，AG=CE，
∴
| PG |
| CG |
| BG |
| CB |
| BG |
| CB |
| PE |
| AG |
∴
| PG |
| CG |
| PE |
| AG |
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
