题目内容
17. 如图,直线AO⊥OB于点O,OT平分∠AOB,则∠AOT=45°.
如图,直线AO⊥OB于点O,OT平分∠AOB,则∠AOT=45°.
分析 由AO⊥OB可得∠AOB=90°,再根据角平分线的定义进行解答即可.
解答 解:∵AO⊥OB,
∴∠AOB=90°,
∵OT平分∠AOB,
∴∠AOT=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
故答案为:45°.
点评 本题主要考查的是垂直与角平分线的定义,掌握角平分线和垂直的定义是解决此题的关键.

练习册系列答案
相关题目
12. 如图所示的立体图形的主视图是( )
如图所示的立体图形的主视图是( )
 如图所示的立体图形的主视图是( )
如图所示的立体图形的主视图是( )| A. |  | B. |  | C. |  | D. |  |
9.下列实数中,属无理数的是( )
| A. | $\frac{22}{7}$ | B. | 1.010010001 | C. | $\sqrt{27}$ | D. | cos60° |
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{169}$ | C. | $\sqrt{{x^2}+4}$ | D. | $\sqrt{\frac{1}{x}}$ |
7. 如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
 如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
如图,已知直线a,b被直线c所截,那么∠1的同位角是( )| A. | ∠5 | B. | ∠4 | C. | ∠3 | D. | ∠2 |
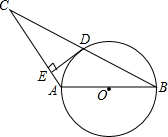 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.