Question

如图，已知矩形ABCD中，AB=10，AD=4，点E为CD边上的一个动点，连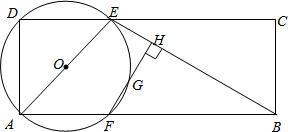接AE、BE，以AE为直径作圆，交AB于点F，过点F作FH⊥BE于H，直线FH交⊙O于点G．
（1）求证：⊙O必经过点D；
（2）若点E运动到CD的中点，试证明：此时FH为⊙O的切线；
（3）当点E运动到某处时，AE∥FH，求此时GF的长．

Answer 1

分析：（1）根据矩形的性质以及直角三角形的性质直角三角形斜边上的中线等于斜边的一半即可得出；
（2）首先根据矩形的判定得出四边形AFED为矩形，进而得出OF为△ABE的中位线，则OF∥EB，利用FH⊥EB，得出OF⊥FH，即可得出答案；
（3）根据相似三角形的判定与性质得出ADE∽△ECB，由相似得：DE=2或8，进而分类讨论得出即可．

解答：证明：（1）如图1，
∵矩形ABCD中，∠ADC=90°，且O为AE中点，
∴OD=

1

2

AE，
∴点D在⊙O上．

（2）证明：如图1，连接OF、EF，
∵AE为⊙O的直径，
∴∠AFE=90°，
∵∠D=∠DAF=90°，
∴四边形AFED为矩形，
∴AF=DE．
∵E为CD的中点，
∴F为AB的中点．
∴OF为△ABE的中位线，
∴OF∥EB．
∵FH⊥EB，
∴OF⊥FH，
又∵OF是⊙O的半径，
∴FH为⊙O的切线．

（3）作OM⊥FG，连接OF，
∵AE∥FH，
∴∠AEB=90°，
易证△ADE∽△ECB，
由相似得：DE=2或8．，
①当DE=2时，
如图2，AF=2，FB=8，EB=4

5

，AE=2

5

，
由△BFH∽△BAE得，
则

HB

BE

=

BF

AB

，
故

HB

4 5

=

8

10

，
解得：HB=

16 5

5

，则OM=EH=BE-HB=

4 5

5

，
FM=

FO2-MO2

=

3 5

5

，
故FG=2FM=

6 5

5

，
②当DE=8时，如图3，同上解法，

可得OG=

1

2

AE=2

5

，OM=EH=

8 5

5

，
故FG=2GM=

12 5

5

．

点评：此题属于圆的综合题目，涉及了切线的判定、中位线的性质及解直角三角形的知识，综合性较强，难度较大，解答本题的关键是熟练掌握各部分的知识，融会贯通．