题目内容
如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E,F,G三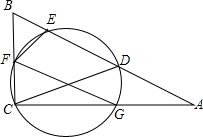 点,连接FE,FG.
点,连接FE,FG.(1)求证:∠EFG=∠B;
(2)若AC=2BC=4
| 5 |
分析:(1)连接DG,首先证DG∥BC,得∠B=∠GDA,再根据圆内接四边形的性质得出∠ADG=∠EFG,经等量代换后可得出∠EFG=∠B;
(2)由勾股定理,易求得AB的长;连接CE,Rt△ACB中,CE⊥AB,由射影定理可求出AE的长,也就求得了DE、BE的长,再根据射影定理可求出CE的值;进而可在Rt△CED中,用勾股定理求出CD的长.
(2)由勾股定理,易求得AB的长;连接CE,Rt△ACB中,CE⊥AB,由射影定理可求出AE的长,也就求得了DE、BE的长,再根据射影定理可求出CE的值;进而可在Rt△CED中,用勾股定理求出CD的长.
解答: (1)证明:连接GD;
(1)证明:连接GD;
∵CD是直径,
∴∠CGD=90°;
∴DG∥BC,
∴∠ADG=∠B;
又∵四边形DGFE是圆的内接四边形,
∴∠ADG=∠EFG;
∴∠B=∠EFG;
(2)解:连接CE,则CE⊥AB;
在Rt△ACB中,AC=4
,BC=2
;
由勾股定理,得:AB=
=10;
由于CE⊥AB,由射影定理,得:AE=AC2÷AB=8;
∴AD=DE=4,BE=2;
CE2=AE•BE=16,∴CE=4;
Rt△CED中,CE=4,DE=4;∴CD=4
.
 (1)证明:连接GD;
(1)证明:连接GD;∵CD是直径,
∴∠CGD=90°;
∴DG∥BC,
∴∠ADG=∠B;
又∵四边形DGFE是圆的内接四边形,
∴∠ADG=∠EFG;
∴∠B=∠EFG;
(2)解:连接CE,则CE⊥AB;
在Rt△ACB中,AC=4
| 5 |
| 5 |
由勾股定理,得:AB=
| AC2+BC2 |
由于CE⊥AB,由射影定理,得:AE=AC2÷AB=8;
∴AD=DE=4,BE=2;
CE2=AE•BE=16,∴CE=4;
Rt△CED中,CE=4,DE=4;∴CD=4
| 2 |
点评:此题主要考查了圆周角定理、圆内接四边形的性质、勾股定理、射影定理等知识的综合应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
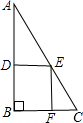 如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )
如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
 6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF
6、如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FG⊥AB,垂足为G,则CF 15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为
15、如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为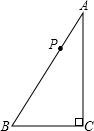 如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有
如图,P为Rt△ABC斜边AB上任意一点(除A、B外),过点P作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有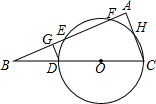 如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G
如图,D为Rt△ABC斜边BC上的一点,以CD为直径作⊙O交边AB于E、F两点,交AC于H,DG⊥AB于点G