题目内容
14.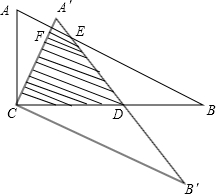 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,将△ABC绕直角顶点C按顺时针方向旋转,得△A′B′C′,斜边A′B′分别与BC、AB相交于点D、E.直角边A′C与AB交于点F,若CD=AC,则△ABC至少旋转30度才能得到△A′B′C.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,将△ABC绕直角顶点C按顺时针方向旋转,得△A′B′C′,斜边A′B′分别与BC、AB相交于点D、E.直角边A′C与AB交于点F,若CD=AC,则△ABC至少旋转30度才能得到△A′B′C.
分析 由旋转的性质得出∠A′=∠A=60°,A′C=AC,证出△A′CD是等边三角形,得出∠A′CD=60°,求出∠ACA′=30°即可.
解答 解:由旋转的性质得:∠A′=∠A=60°,A′C=AC,
∵CD=AC,
∴A′C=CD,
∴△A′CD是等边三角形,
∴∠A′CD=60°,
∵∠ACB=90°,
∴∠ACA′=90°-60°=30°;
故答案为:30.
点评 本题考查了旋转的性质、等边三角形的判定与性质;熟练掌握旋转的性质,证出三角形是等边三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.据国家统计局核算,2014年全年国内生产总值(GDP)超过63个亿,比2013年增长7.4%,数据“63万亿”用科学记数法表示为( )
| A. | 63×104 | B. | 6.3×105 | C. | 6.3×1012 | D. | 6.3×1013 |
9.下列命题中,真命题是( )
| A. | 等边三角形既是轴对称图形又是中心对称图形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 有两条对角线相等的四边形是矩形 |
6.把x2-4x+4分解因式,结果正确的是( )
| A. | (x-2)2 | B. | (x+2)2 | C. | (x-4)2 | D. | (x+4)2 |