äãá¢áÖàï
Àƒäãá¢À¢ä§ƒ¢¤₤ò»![]() çáë¥üµÆŠÅåøò.
çáë¥üµÆŠÅåøò.
ÅÀ뾡ªƒïîÏü¯¤₤ò»çáƒÙîÕȘÑå¤₤ò»![]() çáë¥üµÆŠÅåøò§½ÅÅêù䧃¢.
çáë¥üµÆŠÅåøò§½ÅÅêù䧃¢.
üôûÌòúÅÀêêçá䧃¢¿»°äȘúŠáЯÿûÎý¿°ðëõí«È¤
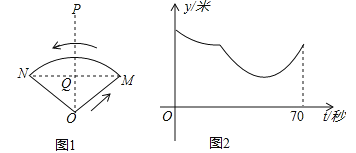
È´1ÈˋüôÝÚòú![]() ÆŠ
ÆŠ![]() çᥡæÕÑåÆÎøç
çᥡæÕÑåÆÎøç
| ÀÙ |
|
|
|
|
|
|
|
|
| ÀÙ |
| ÀÙ |
|
|
|
|
|
|
|
|
| ÀÙ |
å·![]() _______È£
_______È£![]() _______È£
_______È£
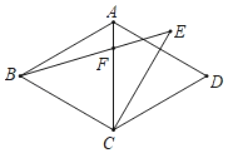
È´2ÈˋåÖó§ûÌøݧúæ½Ýõüç![]() øÅȘûÒ°—ØåèüÝÚøÅ¡¼ÑåÑåÆÎøçöˆæ½ÝõçáçÐȘ¡ªƒïûÒ°—çáçÐȘ£Ù°—¡û¤₤ò»çáë¥üµÈ¤
øÅȘûÒ°—ØåèüÝÚøÅ¡¼ÑåÑåÆÎøçöˆæ½ÝõçáçÐȘ¡ªƒïûÒ°—çáçÐȘ£Ù°—¡û¤₤ò»çáë¥üµÈ¤
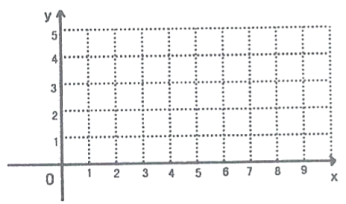
È´3Èˋ§Ã¤ü¤₤ò»ë¥üµÈ˜§ãƒ—öòäãȤçÝ![]() òÝȘøݧÆÅÇ°—ùªÆÅôºæÐä¾¥±çá
òÝȘøݧÆÅÇ°—ùªÆÅôºæÐä¾¥±çá![]() çá§■ùóøçÈ´ƒ¨àñç§
çá§■ùóøçÈ´ƒ¨àñç§![]() Èˋ.
Èˋ.
ÀƒÇÞ¯¡À¢È´1Èˋ![]() È£b
È£b![]() ȣȴ2Èˋë¥üþ¥«§ãö—ȣȴ3Èˋ
ȣȴ2Èˋë¥üþ¥«§ãö—ȣȴ3Èˋ![]() £·
£·![]()
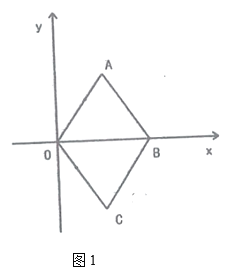
Àƒ§ãö—À¢
È´1Èˋ§¨![]() ÇºàŠ¥Ç¢èúµçûȤ
ÇºàŠ¥Ç¢èúµçûȤ![]() È£§¨
È£§¨![]() ÇºàŠ¥Ç¢èúµçûȤb
ÇºàŠ¥Ç¢èúµçûȤb![]()
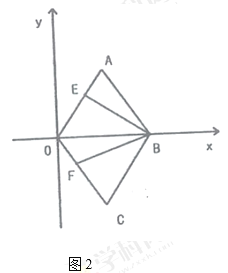
È´2Èˋ§¨ÝÚ¡þøÅçáçÐûÒåÖæ½ÝõüçøÅȘࣤµÆû󧣘çáúºüÔ꘧ƥǢèçûÈ£
È´3Èˋ¡ªƒïë¥üþȘíØ秤₤ò»ë¥üþÆŠy=3íãä¾øÝüÔç᧣çÐȘÅÇ°—§■ùóøç¥Ç¢è
§ãȤȴ1Èˋ§¨![]() ǺàŠ
ǺàŠ![]() çûȤ
çûȤ
ÀÁ![]() È£
È£
§¨![]() ǺàŠ
ǺàŠ![]() çûȤ
çûȤ
ÀÁb![]()
¿òÇÞ¯¡öˆÈ¤![]() È£b
È£b![]()
È´2ÈˋûÒçÐê˜üÔàÓüôë¥

È´3ÈˋÆèë¥üþ¢èøˆÈ˜çÝy=3òÝȘÆÅꧡ—çпÜýšçûôºæÐ![]() çá
çá![]() çá§■ùóøçöˆ
çá§■ùóøçöˆ![]() £·
£·![]()
¿òÇÞ¯¡öˆÈ¤![]() £·
£·![]()

 ÆéîÏû«òÎû«äãüçêÅÇÞ¯¡
ÆéîÏû«òÎû«äãüçêÅÇÞ¯¡Àƒäãá¢À¢![]() áõǤ§ÖóÖ¥ðȘá°öÿØ翨ùƒæÕø₤ꧡ—ÅÀú½çáý¢ñøƒÆûþàËôûÆöȘØîøˆá°ƒ¯çÐçáûéóݥܡþàÓüôÝÚȤ
áõǤ§ÖóÖ¥ðȘá°öÿØ翨ùƒæÕø₤ꧡ—ÅÀú½çáý¢ñøƒÆûþàËôûÆöȘØîøˆá°ƒ¯çÐçáûéóݥܡþàÓüôÝÚȤ
¿¤óÝàùò» |
|
|
|
û¢àùûéóÝ¥Ü |
|
|
|
ÅÀú½Âìçáàùò»èìÆÖ![]() àùȘÅÀú½ÂÖçáàùò»ÑÁÆÖ
àùȘÅÀú½ÂÖçáàùò»ÑÁÆÖ![]() àùúØèìÆÖ
àùúØèìÆÖ![]() àùȘàÓ¿«ê§ÅÀú½çËÑ⿤óÝȘå·Ø£¿ýøÏ¡Ñ
àùȘàÓ¿«ê§ÅÀú½çËÑ⿤óÝȘå·Ø£¿ýøÏ¡Ñ![]() åˆÈ£àÓ¿«ê§ÅÀú½êˆ¤üóÞâÇæ¼öˆØ£¡—ëéäÍ¿¤óÝȘطöˆàùò»°˜¿»
åˆÈ£àÓ¿«ê§ÅÀú½êˆ¤üóÞâÇæ¼öˆØ£¡—ëéäÍ¿¤óÝȘطöˆàùò»°˜¿»![]() àùȘø£ÅÒ£´ñî
àùȘø£ÅÒ£´ñî![]() åˆúŠöòȤ
åˆúŠöòȤ
È´1Èˋꧡ—ÅÀú½¡¼ÆÅÑÁèìàùÈ¢
È´2ÈˋëéäÍ¿¤óÝÆŠçËÑ⿤óÝüÁÝà§üȘꧡ—ÅÀú½¡¼§ÖòÀêùÑÁèìúÛÈ¢
È´3Èˋà¶ÅÀú½ÂìçËÑ⿤óÝȘúŠöˆÅÀú½ÂìèÒ¥óØ£øøæŸòÀúÛçῤô·ñ§¯¡È˜ýÂ¥óùÐáÉòÀÑÁèìåˆúÛÈ¢