题目内容
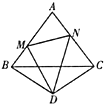
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
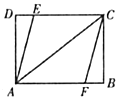
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是菱形,求出菱形的边长.
是菱形,求出菱形的边长.
【答案】(1)见解析;(2)![]()
【解析】
(1)首先根据矩形的性质可得AB平行且等于CD,然后根据DE=BF,可得AF平行且等于CE,即可证明四边形AFCE是平行四边形;
(2)根据四边形AFCE是菱形,可得AE=CE,然后设DE=x,表示出AE,CE的长度,根据相等求出x的值,继而可求得菱形的边长及周长.
(1)∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∵DE=BF,
∴AF=CE,AF∥CE,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是菱形,
∴AE=CE,
设DE=x,
则AE=![]() ,CE=8x,
,CE=8x,
则![]() =8x,
=8x,
化简有16x28=0,
解得:x=![]() ,
,
将x=![]() 代入原方程检验可得等式两边相等,
代入原方程检验可得等式两边相等,
即x=![]() 为方程的解.
为方程的解.
则菱形的边长为:8![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小王根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小亮的探究过程,请你帮忙补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| … |
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
| … |
则![]() _______;
_______;![]() _______;
_______;
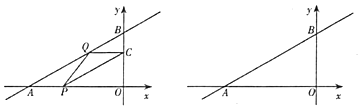
(2)在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
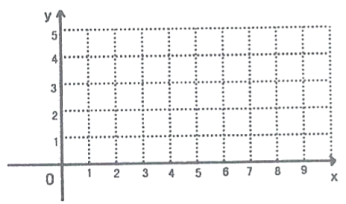
(3)结合函数图象,解决问题:当![]() 时,直接写出所有满足条件的
时,直接写出所有满足条件的![]() 的近似值(精确到
的近似值(精确到![]() ).
).