题目内容
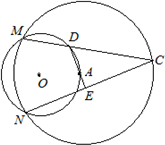 已知:如图,⊙O与⊙A交于M、N点,且点A在⊙O上,弦MC交⊙O于D点,连接AD、NC,并延长DA交NC于E.
已知:如图,⊙O与⊙A交于M、N点,且点A在⊙O上,弦MC交⊙O于D点,连接AD、NC,并延长DA交NC于E.求:∠AEC的度数.
分析:连接MN,OA,AN,MN交OA于B,根据相交两圆的性质求出MN⊥AB,根据圆周角定理求出∠C=∠BAN,根据圆内接四边形性质求出∠CDE=∠ANB,根据三角形的内角和定理求出即可.
解答:解:连接MN,OA,AN,MN交OA于B,
∵MN是公共弦,OA为圆心距,
∴MN⊥OA于B,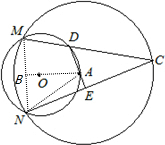
∴∠ABN=90°,
在⊙A中∵∠C的度数等于弧MN的度数的一半,∠BAN的度数也等于弧MN的度数的一半,
∴∠C=∠BAN,
∵M、N、A、D四点共圆,
∴∠ADC=∠BNA,
∵∠BAN+∠BNA=90°,
∴∠C+∠EDC=90°,
∴∠AEC=180°-90°=90°.
答:∠AEC的度数是90°.
∵MN是公共弦,OA为圆心距,
∴MN⊥OA于B,

∴∠ABN=90°,
在⊙A中∵∠C的度数等于弧MN的度数的一半,∠BAN的度数也等于弧MN的度数的一半,
∴∠C=∠BAN,
∵M、N、A、D四点共圆,
∴∠ADC=∠BNA,
∵∠BAN+∠BNA=90°,
∴∠C+∠EDC=90°,
∴∠AEC=180°-90°=90°.
答:∠AEC的度数是90°.
点评:本题主要考查对相交两圆的性质,三角形的内角和定理,圆内接四边形的性质,圆周角定理等知识点的理解和掌握.能求出∠C+∠CDE的度数是解此题的关键.

练习册系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.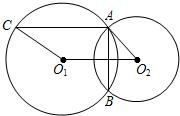 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.