题目内容
16.已知关于x的方程x2+2(k-3)x+k2=0有两个不相等的实数根x1、x2.(1)求k的取值范围;
(2)若|x1+x2-9|=x1x2,求k的值.
分析 (1)由于关于x的方程x2-(2k-3)x+k2=0有两个不相等的实数根,可知△>0,据此进行计算即可;
(2)根据一元二次方程的根与系数的关系可以得到x1+x2=-2(k-3),x1x2=k2,再将它们代入|x1+x2-9|=x1x2,即可求出k的值.
解答 解:(1)∵关于x的方程x2-(2k-3)x+k2=0有两个不相等的实数根,
∴△=[-(2k-3)]2-4k2=-12k+9>0,
解得k<$\frac{3}{4}$.
(2)由根与系数的关系,x1+x2=-2(k-3),x1x2=k2,
∵|x1+x2-9|=x1x2,
∴|-2(k-3)-9|=k2,
化简得k2+2k-3=0,
解得:k=1或k=-3,
又∵k<$\frac{3}{4}$,
∴k=-3.
点评 本题考查了一元二次方程ax2+bx+c=0根的判别式和根与系数的关系的应用,用到的知识点:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根;(4)x1+x2=-$\frac{b}{a}$;(5)x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
6.三角形的外心具有的性质是( )
| A. | 到三个顶点的距离相等 | B. | 到三边的距离相等 | ||
| C. | 是三角形三条角平分线的交点 | D. | 是三角形三条中线的交点 |
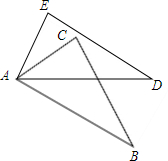 如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.
如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.