题目内容
10.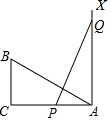 如图,∠C=90°,AC=12,BC=6,AX⊥AC,点P和Q分别在线段AC和射线AX上运动,且PQ=AB,当点P从A点出发运动到C点或AC中点处时,△ABC≌△APQ.
如图,∠C=90°,AC=12,BC=6,AX⊥AC,点P和Q分别在线段AC和射线AX上运动,且PQ=AB,当点P从A点出发运动到C点或AC中点处时,△ABC≌△APQ.
分析 分两种情况:①当AP=BC=5时;②当AP=CA=10时;由HL证明Rt△ABC≌Rt△PQA(HL),即可得出结果.
解答 解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90,
分两种情况:
①当AP=BC=6时,
在Rt△ABC和Rt△QPA中,$\left\{\begin{array}{l}{AB=PQ}\\{BC=AP}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=12时,
在△ABC和△PQA中,$\left\{\begin{array}{l}{AB=PQ}\\{AP=AC}\end{array}\right.$,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=6(此时P为AC的中点或12(此时P和C点重合)时,△ABC与△APQ全等;
故答案为:C点或AC中点.
点评 本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法,本题需要分类讨论,难度适中.

练习册系列答案
相关题目
1.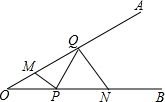 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )| A. | β-α=60° | B. | β+α=210° | C. | β-2α=30° | D. | β+2α=240° |
18.数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1米的竹竿的影长是0.8米,测树高时,这棵树在地面上影长为2.6米,请计算树高为( )米.
| A. | 3.25 | B. | 4.25 | C. | 4.45 | D. | 4.75 |
5.下列各组数是勾股数的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 5,9,12 | D. | 6,9,13 |
1.民兴中学某班教室有50人在开家长会,其中有3名老师,12名家长,35名学生.校长在门外听到有人在发言,
那么发言人是老师或学生的概率为( )
那么发言人是老师或学生的概率为( )
| A. | $\frac{19}{25}$ | B. | $\frac{3}{10}$ | C. | $\frac{47}{50}$ | D. | $\frac{1}{2}$ |
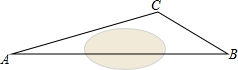 在一次课外实践活动中,数学兴趣小组要测量某公园人工湖两侧A、B两个凉亭之间的距离,如图,现测得∠ABC=30°,∠CAB=15°,AC=300米,请计算A、B两个凉亭之间的距离(结果精确到1米)
在一次课外实践活动中,数学兴趣小组要测量某公园人工湖两侧A、B两个凉亭之间的距离,如图,现测得∠ABC=30°,∠CAB=15°,AC=300米,请计算A、B两个凉亭之间的距离(结果精确到1米)



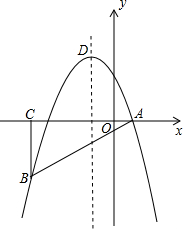 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.