题目内容
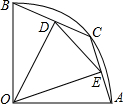 如图,在半径为3的扇形AOB中,∠AOB=90°,点C是弧AB上一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为3的扇形AOB中,∠AOB=90°,点C是弧AB上一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=2时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
考点:垂径定理,勾股定理,三角形中位线定理
专题:
分析:(1)利用垂径定理,在直角△OBD中,利用勾股定理即可求解;
(2)连接AB,由OD垂直于BC,OE垂直于AC,利用垂径定理得到D、E分别为BC、AC的中点,即ED为三角形ABC的中位线,由OA=OB=2,且∠AOB=90°,利用勾股定理求出AB的长,即可求出ED的长.
(2)连接AB,由OD垂直于BC,OE垂直于AC,利用垂径定理得到D、E分别为BC、AC的中点,即ED为三角形ABC的中位线,由OA=OB=2,且∠AOB=90°,利用勾股定理求出AB的长,即可求出ED的长.
解答: 解:(1)∵OD⊥BC,
解:(1)∵OD⊥BC,
∴BD=
BC=1,
在直角△OBD中,OD=
=
=2
;
(2)连接AB,
∵OD⊥BC,OE⊥AC,
∴D、E分别为BC、AC的中点,
∴DE为△ABC的中位线,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB=
=3
则DE=
AB=
.
 解:(1)∵OD⊥BC,
解:(1)∵OD⊥BC,∴BD=
| 1 |
| 2 |
在直角△OBD中,OD=
| OB2-BD2 |
| 32-12 |
| 2 |
(2)连接AB,
∵OD⊥BC,OE⊥AC,
∴D、E分别为BC、AC的中点,
∴DE为△ABC的中位线,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB=
| OA2+OB2 |
| 2 |
则DE=
| 1 |
| 2 |
3
| ||
| 2 |
点评:此题考查了垂径定理,勾股定理,以及三角形的中位线定理,熟练掌握定理是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目




 知观察所A的标高(当水位为0m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m)
知观察所A的标高(当水位为0m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m)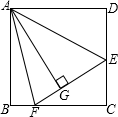 在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.
在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.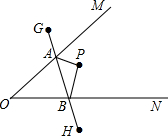 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为 如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.
如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.