题目内容
1.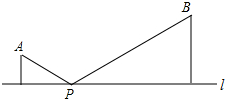 如图,点A,B都在直线l的同一侧,若P为直线l上一点,且满足PA+PB最短为点A到直线l的距离与点B到直线L的距离之和的2倍,则∠APB=120度.
如图,点A,B都在直线l的同一侧,若P为直线l上一点,且满足PA+PB最短为点A到直线l的距离与点B到直线L的距离之和的2倍,则∠APB=120度.
分析 如图所示作点A关于l的对称点A′,连接A′B交l于点P,则PA′+PB=2(A′M+BM),由BN∥MA′,可知$\frac{MA′}{A′P}=\frac{NB}{PB}=\frac{MA′+BN}{A′P+PB}=\frac{1}{2}$,从而可求得∠BPN=∠MPA′=30°,从而可求得∠APB=120°.
解答 解:如图所示:作点A关于l的对称点A′,连接A′B交l于点P.
由轴对称的性质可知;AP=PA′,
∵AP=PA′,
∴PA+PB=P′A+PB=A′P.
∵PA+PB最短为点A到直线l的距离与点B到直线L的距离之和的2倍,
∴$\frac{A′M+BN}{A′P+PB}=\frac{1}{2}$.
∵BN∥MA′,
∴$\frac{MA′}{A′P}=\frac{BN}{PB}=\frac{1}{2}$.
∴∠BPN=∠MPA′=30°,
∴∠APB=120°.
故答案为:120.
点评 本题主要考查的是轴对称--最短路径问题,平行线分线段成比例定理、特殊锐角三角函数值、比例的性质,利用特殊锐角三角函数值求得∠BPN=∠MPA′=30°是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.方程2x2-5x+1=0的解的情况是( )
| A. | 有两个不相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有一个实数根 |
13.某市2012年国内生产总值(GDP)比2011年增长了12%,由于受到国际金融危机的影响,预计2013年比2012年增长7%.若这两年GDP平均增长率为x%,则x%满足的关系是( )
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2•x% | D. | (1+12%)(1+7%)=(1+x%)2 |
10.若a+b+c=2015,则抛物线y=ax2+bx+c必定经过的点是( )
| A. | (-1,-2015) | B. | (1,2015) | C. | (-1,2015) | D. | (1,-2015) |
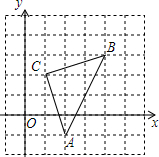 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),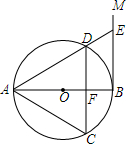 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.