题目内容
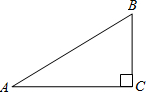如图，在△ABC中，∠C=90°，AB=5，BC=3，则tanA的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：锐角三角函数的定义,勾股定理
专题：
分析：首先利用勾股定理求得AC的长度；然后利用锐角三角函数定义进行解答．
解答：解：如图，∵如图，在△ABC中，∠C=90°，AB=5，BC=3，
∴AC=
=
=4，
∴tanA=
=
．
故选：A．
解：如图，∵如图，在△ABC中，∠C=90°，AB=5，BC=3，∴AC=
| AB2-BC2 |
| 52-32 |
∴tanA=
| BC |
| AC |
| 3 |
| 4 |
故选：A．
点评：本题考查了锐角三角函数的定义和勾股定理．正切：锐角A的对边a与邻边b的比叫做∠A的正切，记作tanA．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
下列各数中，是无理数的是（ ）
| A、7 | ||
| B、0.5 | ||
C、
| ||
| D、0.5151151115…（两个5个之间依次多个1） |
下列说法正确的是（ ）
| A、-6是36的算术平方根 | ||||
| B、±6是36的算术平方根 | ||||
C、
| ||||
D、
|
已知点A（-1，y1）、B（1，y2）在直线y=-2x+3上，则y1与y2的大小关系是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、yl=y2 |
| D、y1与y2的大小关系不确定 |
不等式组
的解集在数轴上表示正确的是（ ）
|
A、 |
B、 |
C、 |
D、 |