题目内容
9.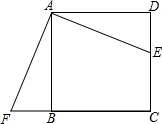 如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB=$\sqrt{3}$,∠EAD=30°,那么点E与点F之间的距离等于$2\sqrt{2}$.
如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB=$\sqrt{3}$,∠EAD=30°,那么点E与点F之间的距离等于$2\sqrt{2}$.
分析 连接EF,证明△AEF是等腰直角三角形,而AE可求,从而EF也就可求.
解答 解:连接EF,如图,
由旋转性质可知:△ADE≌△ABF,
∴AE=AF,∠EAD=∠FAB,
∵∠EAD+∠BAE=90°,
∴∠FAB+∠BAE=90°,
即∠EAF=90°,
∵∠EAD=30°,AB=$\sqrt{3}$,
∴AE=AF=2,
∴EF=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查了正方形的性质、旋转变换的性质、等腰直角三角形的判定与性质、特殊角的三角函数等知识点,难度适中.由旋转的性质得出△AEF是等腰直角三角形是解答本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE.
如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,AF=EF,求证:AC=BE. 画图题:画出此实物的三视图.
画图题:画出此实物的三视图.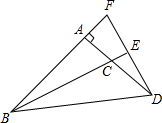 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点A逆时针旋转90°得到Rt△ADF,BC的延长线交DF于点E,连接BD,BC=2EF,求证:BE平分∠DBF.
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点A逆时针旋转90°得到Rt△ADF,BC的延长线交DF于点E,连接BD,BC=2EF,求证:BE平分∠DBF.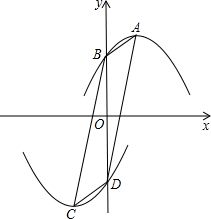 如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.
如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.