题目内容
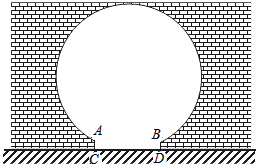某公园的圆弧形门示意图如图所示，已知这个圆弧形门所在的圆的半径为1.5m，圆上A，B两点到水平地面的距离AC=BD=0.4m，AB=1.8m，求圆弧形门的最高点离地面的高度．考点：垂径定理的应用,勾股定理
专题：应用题
分析：首先应弄清最高点在哪儿，即在过圆心作弦AB的垂线与圆的上边的交点，然后将问题转化为求圆的半径，主要运用垂径定理和勾股定理即可．
解答：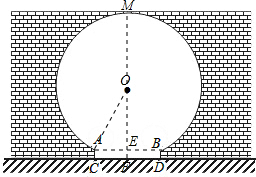
解：过圆心点O作OF⊥CD，交AB于点E，交圆的上部于点M，
∵OE⊥AB，
∴AE=
=0.9m，
设圆O的半径为R，则OE=R-AC=R-0.4，
在Rt△OAE中，AE2+OE2=OA2，
即0.92+（R-0.4）2=R2，
解得：R=1.2125．
则圆弧形门的最高点离地面的高度=OM+OE+EF=1.2125+1.2125-0.4+0.4=2.425m
答：这个圆弧形门的最高点离地面的高度为2.425m．
解：过圆心点O作OF⊥CD，交AB于点E，交圆的上部于点M，∵OE⊥AB，
∴AE=
| AB |
| 2 |
设圆O的半径为R，则OE=R-AC=R-0.4，
在Rt△OAE中，AE2+OE2=OA2，
即0.92+（R-0.4）2=R2，
解得：R=1.2125．
则圆弧形门的最高点离地面的高度=OM+OE+EF=1.2125+1.2125-0.4+0.4=2.425m
答：这个圆弧形门的最高点离地面的高度为2.425m．
点评：本题考查了垂径定理的应用，解答本题的关键是熟练勾股定理的表达式及垂径定理的内容，注意构造直角三角形．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
下列二次根式中，最简二次根式是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
有下列图形：①线段；②角；③三角形；④等边三角形；⑤平行四边形．其中是中心对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
图中的四个小三角形都是等边三角形，边长为2cm，能通过平移△ABC得到其他三角形吗？若能，请画出平移的方向，并说出平移的距离．