题目内容
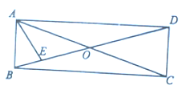
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,把
,把![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() 。再次折叠,使点
。再次折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,点
为折痕,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() 的长为
的长为![]() .
.
【解析】
(1)根据翻折变换的性质可知∠C=∠BAG=90°,PD=AB=CD,∠AGB=∠DGP,故可得出![]() .,可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
.,可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,进而得出tan∠ABG的值;
(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD=![]() AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
AD=4,再根据tan∠ABG即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结论.
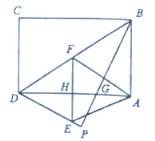
(1)证明:∵△BDP由△BDC翻折而成,
∴∠P=∠BAG=90°,PD=AB=CD,∠AGB=∠DGP,
∴∠ABG=∠ADE,
在△ABG与△C′DG中,
∵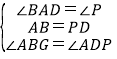 ,
,
∴△ABG≌△C′DG(AAS);.
![]() .
.
设![]() ,则
,则![]() .
.
在![]() 中,可得
中,可得![]() .
.
解得,![]() .
.
![]() .
.
(2)易得![]() 垂直平分
垂直平分![]() ,所以
,所以![]() .
.
由![]() ,可得
,可得![]() .
.
![]() ,解得
,解得![]() .
.
易得![]() 是
是![]() 的中位线,所以
的中位线,所以![]() .
.
![]() 的长为
的长为![]() .
.

练习册系列答案
相关题目