题目内容
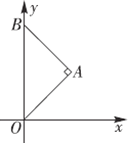
【题目】如图,等腰直角三角形![]() ,
,![]() ,
,![]() 长为
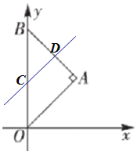
长为![]() ,若直线
,若直线![]() 把
把![]() 分成面积比为
分成面积比为![]() 的两部分,则
的两部分,则![]() 的值为____.
的值为____.
【答案】![]() 或
或![]()
【解析】
根据题意可得A(1,1),求得直线AB的解析式为y=﹣x+2,联立![]() ,求得D点横坐标为
,求得D点横坐标为![]() ,令y=0,得C(0,m),然后分S△BCD=
,令y=0,得C(0,m),然后分S△BCD=![]() 或
或![]() 两种情况,分别求得符合题意的m的值即可.
两种情况,分别求得符合题意的m的值即可.
解:∵等腰直角三角形![]() ,
,![]() ,
,![]() 长为
长为![]() ,
,
∴A(1,1),B(0,2),
设直线AB的解析式为y=kx+b,
将A(1,1),B(0,2)代入解得:y=﹣x+2,
联立![]() ,得﹣x+2
,得﹣x+2![]() ,
,
解得x=![]() ,即D点横坐标为
,即D点横坐标为![]() ,
,
令x=0,则y=m,即C(0,m),
∴BC=2﹣m,
又∵直线![]() 把
把![]() 分成面积比为
分成面积比为![]() 的两部分,
的两部分,
∴当S△BCD=![]() S△ABO时,
S△ABO时,![]() ·
·![]() ·(2﹣m)=
·(2﹣m)=![]() ,
,
解得m=1,或m=![]() (舍去);
(舍去);
当S△BCD=![]() S△ABO时,
S△ABO时,![]() ·
·![]() ·(2﹣m)=
·(2﹣m)=![]() ,
,
解得x=![]() ,或m=5(舍去),
,或m=5(舍去),
综上,m=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目