题目内容
10.观察下面一组等式:①$\sqrt{1-\frac{1}{2}}$=$\sqrt{\frac{1}{2}}$.②$\sqrt{2-\frac{2}{5}}$=2$\sqrt{\frac{2}{5}}$.③$\sqrt{3-\frac{3}{10}}$=3$\sqrt{\frac{3}{10}}$.④$\sqrt{4-\frac{4}{17}}$=4$\sqrt{\frac{4}{17}}$,…,按上述规律.
(1)写出第5个等式;
(2)猜想第n个等式,并给予验证.
分析 (1)根据前四个等式的规律解答;
(2)根据题意总结规律,根据二次根式的性质证明即可.
解答 解:(1)第5个等式:$\sqrt{5-\frac{5}{26}}$=5$\sqrt{\frac{5}{26}}$;
(2)第n个等式:$\sqrt{n-\frac{n}{{n}^{2}+1}}$=n$\sqrt{\frac{n}{{n}^{2}+1}}$,
证明:$\sqrt{n-\frac{n}{{n}^{2}+1}}$=$\sqrt{\frac{{n}^{3}+n}{{n}^{2}+1}-\frac{n}{{n}^{2}+1}}$=$\sqrt{\frac{{n}^{3}}{{n}^{2}+1}}$=n$\sqrt{\frac{n}{{n}^{2}+1}}$.
点评 本题考查的是二次根式的化简,掌握二次根式的性质是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
20.下列说法中,不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 绝对值最小的数是1 | ||
| C. | 一个有理数不是整数就是分数 | D. | 0的相反数是0 |
1.下列计算中正确的有( )个
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.下面图形中,为中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
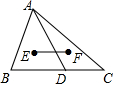 如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.
如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2. 如图所示,正方形卡片A类、B类和长方形卡片C类各若干张,现有A类4张,B类9张,C类13张,如果要拼一个面积最大的正方形,则该正方形边长为2a+3b,但C类卡片还剩1张.
如图所示,正方形卡片A类、B类和长方形卡片C类各若干张,现有A类4张,B类9张,C类13张,如果要拼一个面积最大的正方形,则该正方形边长为2a+3b,但C类卡片还剩1张.