题目内容
在平面直角坐标系中,已知点A(0,2),B(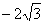 ,0),C(0,-2),D(
,0),C(0,-2),D(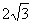 ,0),则以这四个点为顶 点的四边形ABCD是( )。
,0),则以这四个点为顶 点的四边形ABCD是( )。
A.矩形 B.菱形 C.正方形 D.梯形
B

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
题目内容
在平面直角坐标系中,已知点A(0,2),B(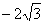 ,0),C(0,-2),D(
,0),C(0,-2),D(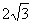 ,0),则以这四个点为顶 点的四边形ABCD是( )。
,0),则以这四个点为顶 点的四边形ABCD是( )。
A.矩形 B.菱形 C.正方形 D.梯形
B

 金钥匙试卷系列答案
金钥匙试卷系列答案