题目内容
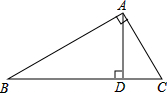如图，在△ABC中，∠BAC=90°，AB=8，AC=6，AD⊥BC，垂足为D，则△ABC斜边上的高AD=考点：勾股定理,三角形的面积
专题：
分析：首先利用勾股定理得出BC的长，再利用三角形面积求法得出AD的长．
解答：解：∵∠BAC=90°，AB=8，AC=6，
∴BC=
=10，
∵AD⊥BC，
∴6×8=AD×10，
解得：AD=4.8．
故答案为：4.8．
∴BC=
| AB2+AC2 |
∵AD⊥BC，
∴6×8=AD×10，
解得：AD=4.8．
故答案为：4.8．
点评：此题主要考查了勾股定理以及三角形面积求法，得出BC的长是解题关键．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
如图，BD是⊙O的直径，点A在BD的延长线上，AC切⊙O于点C，∠A=30°，则∠B=（ ）| A、60° | B、30° |
| C、15° | D、45° |
设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去…根据以上规律，第n个正方形的边长an=6tan45°的值等于（ ）
A、6
| ||
B、3
| ||
| C、6 | ||
D、2
|
一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜0；②a＞0；③当x＜1时，y2＜0；④当x＜3时，y1＜y2中正确的个数是（ ）