题目内容
6.正方形ABCD的边长是4,P是AD边的中点,点E在正方形边上(与顶点不重合),若△PBE是等腰三角形,则底边长为2$\sqrt{2}$或2$\sqrt{5}$.分析 本题分两种情况讨论:(1)当PB为腰时,若P为顶点,则E点和C点重合,此种情况不符合要求;若B为顶点,则E点为CD中点,进而可求出底PE的长;
(2)当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E,由点E不与点A、C重合,根据勾股定理即可找出底PB的长.
解答 解:△PBE为等腰三角形分两种情况: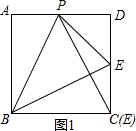
(1)当PB为腰时,如图1所示.
若点P为顶点,
∵点P为AD边的中点,
∴点E与点C重合(舍去);
若点B为中点,
∵四边形ABCD为正方形,点P为AD边的中点,
∴点E为边CD的中点,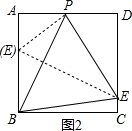
∴DP=DE=$\frac{1}{2}$AB=2,
∴PE=$\sqrt{D{P}^{2}+D{E}^{2}}$=2$\sqrt{2}$;
(2)当PB为底时,如图2所示.
∵点E不与顶点重合,且点P为AD边的中点,
∴AP=$\frac{1}{2}$AD=2,
∴PB=$\sqrt{P{A}^{2}+A{B}^{2}}$=2$\sqrt{5}$.
综上可知:等腰△PBE的底边长为2$\sqrt{2}$或2$\sqrt{5}$.
故答案为:2$\sqrt{2}$或2$\sqrt{5}$.
点评 本题考查了正方形的性质、勾股定理以及等腰三角形的性质,解题的关键是分PB为腰以及PB为底两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,依照题意画出图形,利用数形结合解决问题是关键.

练习册系列答案
相关题目
14.同时投掷2颗均匀的骰子,朝上一面点数的和是偶数的概率是( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
15.在-6,2.0$\stackrel{.}{3}$,$\frac{\sqrt{6}}{2}$,$\sqrt{5}$,π-1,$\frac{3}{7}$中无理数的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.对于单项式5πR2,下列说法正确的是( )
| A. | 系数为5 | B. | 系数为5π | C. | 次数为3 | D. | 次数为4 |
18.下列各组数中,以a,b,c为边长三角形不能组成直角三角形的是( )
| A. | a=1.5,b=2,c=3 | B. | a=5,b=12,c=13 | C. | a=6,b=8,c=10 | D. | a=3,b=4,c=5 |
15.若从一个多边形的一个顶点出发,最多可以引2010条对角线,则它是( )
| A. | 2013边形 | B. | 2012边形 | C. | 2011边形 | D. | 2000边形 |