题目内容
【题目】如图，已知抛物线y＝ax2+
x+c经过A（4，0），B（1，0）两点，与y轴交于点C．
（1）求该抛物线的解析式；
（2）在直线AC上方的抛物线上是否存在一点D，使得△DCA的面积最大？若存在，求出点D的坐标及△DCA面积的最大值；若不存在，请说明理由．
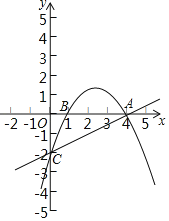
【答案】（1）
；（2）存在，当D（2，1），△DAC面积的最大值为4．
【解析】
（1）由抛物线经过A（4，0），B（1，0），C（0，-2）三点，利用待定系数法即可求得该抛物线的解析式；
（2）设D点的横坐标为t（0＜t＜4），则D点的纵坐标为-
t2+
t-2，过D作y轴的平行线交AC于E．即可求得DE的长，继而可求得S△DCA=-（t-2）2+4，然后由二次函数的性质，即可求得点D的坐标及△DCA面积的最大值．
解：（1）将点A（4，0）、B（1，0）代入抛物线解析式得：
，
解得：
，
则抛物线解析式为；
存在．
如图1，设D点的横坐标为t（0＜t＜4），则D点的纵坐标为﹣t2+t﹣2．
过D作y轴的平行线交AC于E．
设直线AC的解析式为：y＝mx+n，
则 
，
解得：
，
由题意可求得直线AC的解析式为y＝x﹣2．
∴E点的坐标为（t，t﹣2）．
∴DE＝﹣t2+t﹣2﹣（t﹣2）＝﹣t2+2t．
∴S△DCA＝S△CDE+S△ADE＝×DE×OA＝×（﹣t2+2t）×4＝﹣t2+4t＝﹣（t﹣2）2+4．
∴当t＝2时，S最大＝4．
∴当D（2，1），△DAC面积的最大值为4．
名校课堂系列答案
【题目】去年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为
，
，
，
四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（ | 频数（人数） |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
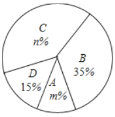
根据以上信息，解答以下问题：
（1）表中的
；
（2）扇形统计图中
，
，等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得等级6名学生中选取两人做为学校“五好小公民”志愿者，已知这6人中有3名男生（用
，
，
表示）和3名女生（用
，
，
表示），请用列表或画树状图的方法求恰好选取的是和的概率．
