Question

【题目】矩形ABCD中，E，F在BC、CD上，以EF为直径的半圆切AD于G（如图1）．

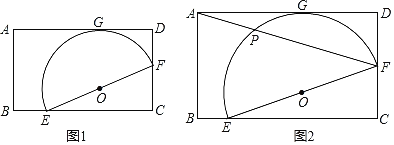
（1）求证：CE＝2DG；

（2）若F为DC中点，连AF交半圆于P（如图2），且AB＝4，AD＝5，求PF．

Answer 1

【答案】（1）详见解析；（2）2．

【解析】

（1)连接OG，延长GO交BC于H，由切线的性质得出OG⊥AD，证明四边形CDGH是矩形，得出DG＝CH，GH＝CD，由平行线得出EH＝CH，即可得出结论；

（2）连接OG，延长GO交BC于H，由勾股定理得出AF3，由（1）得：CE＝2DG，EH＝CH，GH＝CD＝AB＝4，证明OH是△CEF的中位线，得出OHCF＝1，OG＝GH﹣OH＝3，得出EF＝2OG＝6，由勾股定理得出CE4，DGCE＝2，得出AG＝AD﹣DG＝3，由切割线定理求出AP，即可得出结果．

(1)证明：连接OG，延长GO交BC于H，如图所示：

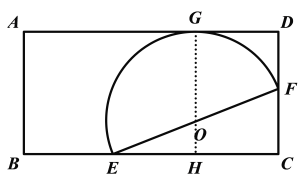
∵以EF为直径的半圆切AD于G，

∴OG⊥AD，

∵四边形ABCD是矩形，

∴∠D＝90°，AB＝CD，AD∥BC，AD⊥CD，

∴GH∥CD，

∴四边形CDGH是矩形，

∴DG＝CH，GH＝CD，

∵OE＝OF，

∴EH＝CH，

∴CE＝2DG；

(2)解：连接GP，GF，OG，延长GO交BC于H，如下图所示：

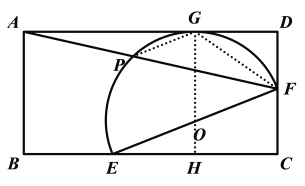
∵F为DC中点，∴DF＝CFCD＝2，

∴AF3，

由（1）得：CE＝2DG，EH＝CH，GH＝CD＝AB＝4，

∵OE＝OF，

∴OH是△CEF的中位线，

∴OHCF＝1，

∴OG＝GH﹣OH＝3，

∴EF＝2OG＝6，

∴CE4，

∴DGCE＝2，

∴AG＝AD﹣DG＝3，

∵以EF为直径的半圆切AD于G，

故由弦切角定理可知：∠AGP=∠PFG，

由∠GAF=∠GAF，

∴△AGP∽△AFG，

∴

∴AG2＝AP×AF，

∴AP，

∴PF＝AF-AP＝32．

故答案为：2．