题目内容
3.若不等式组$\left\{\begin{array}{l}{x+a<3}\\{x-2b>4}\end{array}\right.$的解集为-2<x<0,则a+b=( )| A. | 0 | B. | 3 | C. | -9 | D. | 6 |
分析 首先计算出两个不等式的解集,再根据不等式组的解集为-2<x<0可得3-a=0,2b+4=-2,再解出a、b的值,进而可得答案.
解答 解:$\left\{\begin{array}{l}{x+a<3①}\\{x-2b>4②}\end{array}\right.$,
由①得:x<3-a,
由②得:x>2b+4,
∵解集为-2<x<0,
∴3-a=0,2b+4=-2,
解得:a=3,b=-3,
∴a+b=0,
故选:A.
点评 此题主要考查了解一元一次不等式组,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
15.下面关于二次根式$\sqrt{9-2x}$的说法正确的是( )
| A. | 没有最大值,最小值为0 | B. | 没有最大值,没有最小值 | ||
| C. | 最大值为3,最小值为0 | D. | 最大值为3,没有最小值 |
 如图,正方形的边长为4,则图中阴影部分的面积为16-4π.
如图,正方形的边长为4,则图中阴影部分的面积为16-4π.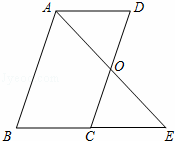 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.