题目内容
13.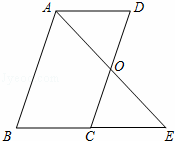 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当AE与CD满足什么关系时,四边形ACED是正方形?请说明理由.
分析 (1)首先根据O是CD的中点,可得DO=CO,再证明∠D=∠OCE,然后可利用ASA定理证明△AOD≌△EOC;
(2)欲四边形ACED是正方形,需要推知四边形ACED为平行四边形,利用“对角线相等且相互平分的平行四边形为正方形”得到AE⊥CD且AE=CD.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
$\left\{\begin{array}{l}{∠D=∠OCE}\\{∠DAO=∠CEO}\\{DO=CO}\end{array}\right.$,
∴△AOD≌△EOC(AAS);
(2)当AE⊥CD且AE=CD时,四边形ACED是正方形.
证明:∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵AE⊥CD
∴?ACED是菱形.
∵AE=CD,
∴菱形ACED是正方形.
点评 此题主要考查了全等三角形的判定与性质,以及正方形的判定,关键是掌握“对角线相等且相互平分的平行四边形为正方形”.

练习册系列答案
相关题目
4. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )| A. | 120mm2 | B. | 135mm2 | C. | 108mm2 | D. | 96mm2 |
8.下列计算中正确的是( )
| A. | $\sqrt{2}$+$\sqrt{6}$=$\sqrt{8}$ | B. | 2+$\sqrt{3}$=2$\sqrt{3}$ | C. | $\sqrt{3}$•$\sqrt{5}$=$\sqrt{15}$ | D. | $\frac{\sqrt{4}}{2}$=2 |
 如图,在⊙O中,弦AB=1cm,圆周角∠ACB=30°,则⊙0的直径为2cm.
如图,在⊙O中,弦AB=1cm,圆周角∠ACB=30°,则⊙0的直径为2cm.