题目内容
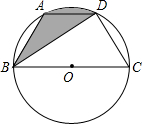 如图,已知点A、B、C、D均在半径为3的已知圆上,AD∥BC,BD平分∠ABC,∠C=60°.
如图,已知点A、B、C、D均在半径为3的已知圆上,AD∥BC,BD平分∠ABC,∠C=60°.(1)求四边形ABCD的周长.
(2)求图中阴影部分的面积(结果保留π).
考点:扇形面积的计算,圆心角、弧、弦的关系
专题:
分析:(1)先根据平行线的性质得出
=
,故可得出∠ABC=∠C=60°,连接OA,OB,可得出△OCD,△OAB与△OAD均为等边三角形,故可得出AD=AB=CD=3,由此可得出结论;
(2)由(1)知,AD=AB=OB=OA=3,故可得出四边形ABOD是菱形,再由SAS定理得出△ABE≌△ODE,故S阴影=S扇形AOD,由此可得出结论.
 |
| AB |
 |
| CD |
(2)由(1)知,AD=AB=OB=OA=3,故可得出四边形ABOD是菱形,再由SAS定理得出△ABE≌△ODE,故S阴影=S扇形AOD,由此可得出结论.
解答: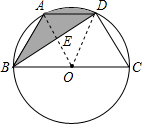 解:(1)∵AD∥BC,∠C=60°,
解:(1)∵AD∥BC,∠C=60°,
∴
=
,
∴∠ABC=∠C=60°.
连接OA,OB,
∵OC=OD=3,∠C=60°,
∴△OCD是等边三角形.
同理可得,△OAB与△OAD均为等边三角形,
∴AD=AB=CD=3,
∴四边形ABCD的周长=BC+CD+AD+AB=6+3+3+3=15;
(2)∵由(1)知,AD=AB=OB=OA=3,
∴四边形ABOD是菱形,
∴AE=OE,BE=DE,
在△ABE与△ODE中,
∵
∴△ABE≌△ODE(SAS),
∴S阴影=S扇形AOD=
=
.
 解:(1)∵AD∥BC,∠C=60°,
解:(1)∵AD∥BC,∠C=60°,∴
 |
| AB |
 |
| CD |
∴∠ABC=∠C=60°.
连接OA,OB,
∵OC=OD=3,∠C=60°,
∴△OCD是等边三角形.
同理可得,△OAB与△OAD均为等边三角形,
∴AD=AB=CD=3,
∴四边形ABCD的周长=BC+CD+AD+AB=6+3+3+3=15;
(2)∵由(1)知,AD=AB=OB=OA=3,
∴四边形ABOD是菱形,
∴AE=OE,BE=DE,
在△ABE与△ODE中,
∵
|
∴△ABE≌△ODE(SAS),
∴S阴影=S扇形AOD=
| 60π×32 |
| 360 |
| 3π |
| 2 |
点评:本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数.
某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数. 如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0).
如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0).
 如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN=
如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN= 如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件:
如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件: