题目内容
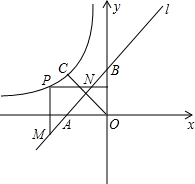 如图,直线l:y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=
如图,直线l:y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=| k |
| x |
(1)求出点A、B两点的坐标及∠BAO的度数;
(2)求反比例函数的解析式;
(3)求AN•BM的值.
考点:反比例函数综合题
专题:
分析:(1)连接AC,BC,由题意得:四边形AOBC为正方形,对于一次函数解析式,分别令x与y为0求出对于y与x的值,确定出OA与OB的值,得到A、B两点的坐标,然后根据三角函数求出∠BAO的度数;
(2)由(1)中条件,求出C的坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)过M作ME⊥y轴,作ND⊥x轴,根据P在反比例解析式上,设出P坐标得出ND的长,根据三角形AND为等腰直角三角形表示出AN与BM的长,即可求出所求式子的值.
(2)由(1)中条件,求出C的坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)过M作ME⊥y轴,作ND⊥x轴,根据P在反比例解析式上,设出P坐标得出ND的长,根据三角形AND为等腰直角三角形表示出AN与BM的长,即可求出所求式子的值.
解答: 解:(1)连接AC,BC,
解:(1)连接AC,BC,
∵y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.
∴OA=OB=1,
∴OC与AB互相平分,且垂直,相等,
∴四边形AOBC为正方形,
对于一次函数y=x+1,令x=0,求得:y=1;令y=0,求得:x=-1,
∴OA=OB=1,
∴A(-1,0),B(0,1),
∴tan∠BAO=
=1,
∴∠BAO=45°,
(2)由(1)得,
∴C(-1,1),
将C(-1,1)代入y=
得:1=
,即k=-1,
则反比例函数解析式为y=-
;
(3)过M作ME⊥y轴,作ND⊥x轴,
设P(a,-
),可得ND=-
,ME=|a|=-a,
∵△AND和△BME为等腰直角三角形,
∴AN=
×(-
)=-
,BM=-
a,
则AN•BM=-
•(-
a)=2.
 解:(1)连接AC,BC,
解:(1)连接AC,BC,∵y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.
∴OA=OB=1,
∴OC与AB互相平分,且垂直,相等,
∴四边形AOBC为正方形,
对于一次函数y=x+1,令x=0,求得:y=1;令y=0,求得:x=-1,
∴OA=OB=1,
∴A(-1,0),B(0,1),
∴tan∠BAO=
| 1 |
| 1 |
∴∠BAO=45°,
(2)由(1)得,
∴C(-1,1),
将C(-1,1)代入y=
| k |
| x |
| k |
| -1 |
则反比例函数解析式为y=-
| 1 |
| x |
(3)过M作ME⊥y轴,作ND⊥x轴,
设P(a,-
| 1 |
| a |
| 1 |
| a |
∵△AND和△BME为等腰直角三角形,
∴AN=
| 2 |
| 1 |
| a |
| ||
| a |
| 2 |
则AN•BM=-
| ||
| a |
| 2 |
点评:本题主要考查了一次函数与反比例函数的交点问题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,以及等腰直角三角形的性质,熟练掌握待定系数法是解本题的关键,同时要充分利用图形解答.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
将分式方程1-
=
去分母,得到正确的整式方程是( )
| 2x |
| x-1 |
| 3 |
| x-1 |
| A、1-2x=3 |
| B、x-1-2x=3 |
| C、1+2x=3 |
| D、x-1+2x=3 |
 如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是
如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是 在平面直角坐标系xOy中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作lPBM.
在平面直角坐标系xOy中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作lPBM.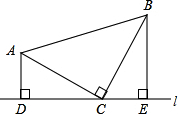 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
 如图是直角坐标中某抛物线的部分图象,请写出抛物线与x轴左边交点的坐标
如图是直角坐标中某抛物线的部分图象,请写出抛物线与x轴左边交点的坐标