题目内容
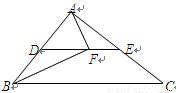
 如图,DE为△ABC边BC的垂直平分线,交BC于E,交AB于点D且∠B=40°,
如图,DE为△ABC边BC的垂直平分线,交BC于E,交AB于点D且∠B=40°,∠A=60°,则∠ACD的度数为
40°
40°
.分析:先根据三角形内角和定理求出∠ACB的度数,再由线段垂直平分线的性质求出∠BCD的度数,根据∠ACD=∠ACB-∠BCD即可得出结论.
解答:解:∵∠B=40°,∠A=60°,
∴∠ACB=180°-60°-40°=80°,
∵DE为△ABC边BC的垂直平分线,
∴∠BCD=∠B=40°,
∴∠ACD=∠ACB-∠BCD=80°-40°=40°.
故答案为:40°.
∴∠ACB=180°-60°-40°=80°,
∵DE为△ABC边BC的垂直平分线,
∴∠BCD=∠B=40°,
∴∠ACD=∠ACB-∠BCD=80°-40°=40°.
故答案为:40°.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为 已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,求证:AN=BM.
已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,求证:AN=BM.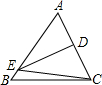 如图,DE为△ABC中AC边的中垂线,BC=8,AB=10,则△EBC的周长是( )
如图,DE为△ABC中AC边的中垂线,BC=8,AB=10,则△EBC的周长是( )