题目内容
已知，如图，DE为△ABC的边AB的垂直平分线，CD为△ABC的外角平分线，与DE交于D，DM⊥BC于M，DN⊥AC于N，求证：AN=BM．分析：根据垂直平分线的性质可得AD=BD，根据角平分线的性质可得DN=DM，然后根据HL即可证得Rt△ADN≌Rt△BDM，根据全等三角形的对应边相等即可证得．
解答：
证明：∵DE为△ABC的边AB的垂直平分线，
∴AD=BD，
∵CD为△ABC的外角平分线，与DE交于D，DM⊥BC于M，DN⊥AC于N，
∴DN=DM，
在Rt△ADN和Rt△BDM中，
，
∴Rt△ADN≌Rt△BDM（HL），
∴AN=BM．
证明：∵DE为△ABC的边AB的垂直平分线，∴AD=BD，
∵CD为△ABC的外角平分线，与DE交于D，DM⊥BC于M，DN⊥AC于N，
∴DN=DM，
在Rt△ADN和Rt△BDM中，
|
∴Rt△ADN≌Rt△BDM（HL），
∴AN=BM．
点评：本题考查了全等三角形的性质和判定，线段的垂直平分线定理，角平分线性质等知识点，会添加适当的辅助线，会利用中垂线的性质找出全等的条件是解此题的关键．
练习册系列答案
相关题目
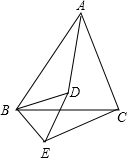已知，如图，D为△ABC内一点连接BD、AD，以BC为边在△ABC外作∠CBE=∠ABD，∠BCE=∠BAD，BE、
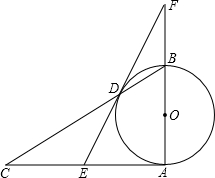（2013•鄂州）已知：如图，AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．
已知：如图，AB为半圆O的直径，C、D是半圆上的两点，E是AB上除O外的一点，AC与DE交于点F．①
