Question

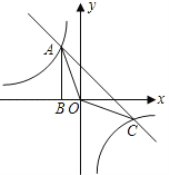
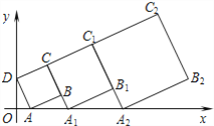
【题目】在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1,………按这样的规律进行下去，正方形A2018B2018C2018C2017的面积为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】试题分析：∵点A的坐标为（1，0），点D的坐标为（0，2），

∴OA＝1，OD＝2，

设正方形的面积分别为S1，S2…S2019，

在直角△ADO中，根据勾股定理，

得：AD＝＝，

∴AB＝AD＝BC＝，

∴正方形ABCD的面积为：S1＝5；

∵∠DAO＋∠ADO＝90°，∠DAO＋∠BAA1＝90°，

∴∠ADO＝∠BAA1，

∵∠AOD＝∠ABA1＝90°，

∴△AOD∽△ABA1，

∴，

即，

∴BA1＝，

∴A1C＝BC＋ BA1＝，

∴正方形A1B1C1C的面积为：S2＝×5＝5×，

根据题意，得：AD∥BC∥C1A2∥C2B2，

∴∠BAA1＝∠B1A1A2＝∠B2A2x，

∵∠ABA1＝∠A1B1A2＝90°，

∴△BAA1∽△B1A1A2，

∴，

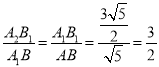∴A2B1＝＝，

∴A2C1＝B1C1＋A2B1＝＋＝，

∴正方形A2B2C2C1的面积为：S3＝×5＝5×，

由此可得：Sn＝5×，

∴正方形A2018B2018C2018C2017的面积为S2019＝5×＝5×．

故选C．