题目内容
抛物线![]() 中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+b上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+b上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
(1)求k的值;
(2)求证:这条抛物线经过点A;
(3)经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点,经过点M作x轴的平行线和直线y=mx+n交于点B,经过点B作x轴的垂线和这条抛物线交于点C,和直线y=kx+1交于点D,探索CD和BC的数量关系.

(1)k=1……………………… (1分)
(2)将顶点M坐标代入y=x+1化简得:(4c-4)a=b2-2b………………… (3分)
∵无论a为和何值,等式都成立,所以4c-4=0,b2-2b=0
∴c=1,b=2
(也可以取两个特殊值得到点M的坐标,代入直线表达式求出b,c的值)
∴抛物线经过点A……………………… (5分)
(3)由题意:方程mx+1=ax2+2x+1的△=0,
∴(2-m)2=0,m=2………………………(7分)
∴点B,C,D的坐标分别是B(-![]() ,
,![]() ),C(-
),C(-![]() ,
, ![]() ),D(-
),D(-![]() ,
,![]() );……… (10分)
);……… (10分)
用a表示出BC,CD的长度,得到BC=CD=|![]() |………………… (12分)
|………………… (12分)
(求出BC=-![]() 或
或![]() 不扣分)
不扣分)

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
抛物线![]() 中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+b上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+b上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
(1)求k的值;
(2)求证:这条抛物线经过点A;

|
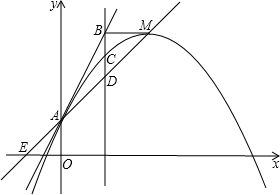 (2013•宜昌模拟)抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
(2013•宜昌模拟)抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE. 抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.
抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.