题目内容
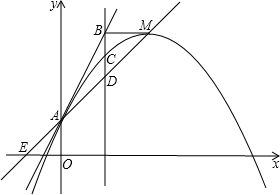（2013•宜昌模拟）抛物线y=ax2+bx+c中，b，c是非零常数，无论a为何值（0除外），其顶点M一定在直线y=kx+1上，这条直线和x轴，y轴分别交于点E，A，且OA=OE．（1）求k的值；
（2）求证：这条抛物线经过点A；
（3）经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点，经过点M作x轴的平行线和直线y=mx+n交于点B，经过点B作x轴的垂线和这条抛物线交于点C，和直线y=kx+1交于点D，探索CD和BC的数量关系．
分析：（1）根据直线解析式可得点A的坐标为（0，1），则可得点E的坐标为（-1，0），代入直线解析式，可求出k的值．
（2）将顶点M的坐标代入直线解析式，再由无论a为何值（0除外），其顶点M一定在直线y=kx+1上，可得出b、c的值，继而可判断这条抛物线经过点A．
（3）根据抛物线与直线只有一个交点，求出m的值，继而得出B、C、D的坐标，求出BC、CD的长度，即可得出CD和BC的数量关系．
（2）将顶点M的坐标代入直线解析式，再由无论a为何值（0除外），其顶点M一定在直线y=kx+1上，可得出b、c的值，继而可判断这条抛物线经过点A．
（3）根据抛物线与直线只有一个交点，求出m的值，继而得出B、C、D的坐标，求出BC、CD的长度，即可得出CD和BC的数量关系．
解答：解：（1）∵直线解析式为y=kx+b，
∴点A的坐标为（0，b），
又∵OA=OE
∴点E的坐标为（-b，0），
将点E的坐标代入直线解析式可得：0=-kb+b，
解得：k=1；
（2）将顶点M的坐标为（
，
）代入y=x+1化简得：（4c-4）a=b2-2b，
∵无论a为和何值，等式都成立，所以4c-4=0，b2-2b=0，
∴c=1，b=2，
即抛物线解析式为y=ax2+2x+1，
将点A（0，1）代入抛物线解析式可得：1=1，
∴抛物线经过点A．
（3）由题意：方程mx+1=ax2+2x+1的△=0，
即（2-m）2=0，
解得：m=2，
故可得点B，C，D的坐标分别是B（-
，
），C（-
，
），D（-
，
），
则可得BC=CD=|
|．
∴点A的坐标为（0，b），
又∵OA=OE
∴点E的坐标为（-b，0），
将点E的坐标代入直线解析式可得：0=-kb+b，
解得：k=1；
（2）将顶点M的坐标为（
| -b |
| 2a |
| 4ac-b2 |
| 4a |
∵无论a为和何值，等式都成立，所以4c-4=0，b2-2b=0，
∴c=1，b=2，
即抛物线解析式为y=ax2+2x+1，
将点A（0，1）代入抛物线解析式可得：1=1，
∴抛物线经过点A．
（3）由题意：方程mx+1=ax2+2x+1的△=0，
即（2-m）2=0，
解得：m=2，
故可得点B，C，D的坐标分别是B（-
| 1 |
| 2a |
| a-1 |
| a |
| 1 |
| 2a |
| 4a-3 |
| 4a |
| 1 |
| 2a |
| 2a-1 |
| 2a |
则可得BC=CD=|
| 1 |
| 4a |
点评：本题考查了二次函数的综合题，涉及了待定系数法求函数解析式、抛物线与直线的交点问题，同学们注意培养自己解决综合题的能力，将所学知识融会贯通．
练习册系列答案
相关题目
（2013•宜昌模拟）已知实数a，b在数轴上的位置如图所示，下列式子的值为正数的是（ ）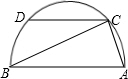
（2013•宜昌模拟）如图，AB是半圆的直径，弦CD∥AB，∠A=65°，∠BCD的度数是（ ）