题目内容
如图,C为半圆⊙O上一点,AB为直径,且AB=2a,∠COA=60°.延长AB到P,使BP= AB,连CP交半圆于D,过P作AP的垂线交AD的延长线于H,则PH的长度为 .
AB,连CP交半圆于D,过P作AP的垂线交AD的延长线于H,则PH的长度为 .
【答案】分析:如图,连接BD,BH;根据直径所对的圆周角是直角,得∠ADB=90°,又∠APH=90°,则四边形PHDB有一个外接圆,所以∠PBH=∠PDH=∠ADC= ∠AOC=30°,在Rt△PHD中利用三角函数即可求出PH.
∠AOC=30°,在Rt△PHD中利用三角函数即可求出PH.
解答: 解:如图,连接BD,BH,
解:如图,连接BD,BH,
∵AB为直径,
∴∠ADB=90°;
又∠APH=90°,
则P、H、D、B四点共圆,
∴∠PBH=∠PDH=∠ADC= ∠AOC=30°,
∠AOC=30°,
∴Rt△PHD中,PH= =
= a.
a.
故填空答案: a.
a.
点评:此题主要是发现能够把要求的线段放到一个30°的直角三角形中,综合运用了圆内接四边形的判定方法以及圆周角定理.
 ∠AOC=30°,在Rt△PHD中利用三角函数即可求出PH.
∠AOC=30°,在Rt△PHD中利用三角函数即可求出PH.解答:
 解:如图,连接BD,BH,
解:如图,连接BD,BH,∵AB为直径,
∴∠ADB=90°;
又∠APH=90°,
则P、H、D、B四点共圆,
∴∠PBH=∠PDH=∠ADC=
 ∠AOC=30°,
∠AOC=30°,∴Rt△PHD中,PH=
 =
= a.
a.故填空答案:
 a.
a.点评:此题主要是发现能够把要求的线段放到一个30°的直角三角形中,综合运用了圆内接四边形的判定方法以及圆周角定理.

练习册系列答案
相关题目
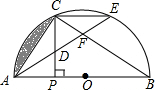 D、F.
D、F. P交半圆于D,过P作AP的垂线交AD的延长线于H,则PH的长度为
P交半圆于D,过P作AP的垂线交AD的延长线于H,则PH的长度为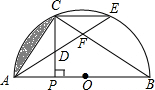 D、F.
D、F.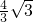 ,∠CAE=30°,求阴影部分的面积.
,∠CAE=30°,求阴影部分的面积.