题目内容
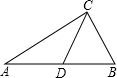如图所示，若CD是△ABC的中线，S△ADC=4，则S△CDB=________．
4
分析：根据三角形的中线定义得点D是AB的中点，所以AD=BD，再根据两三角形的高是同一条高，可得两三角形的面积相等．
解答：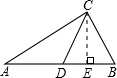
解：∵CD是△ABC的中线，
∴D是AB的中点，
∴AD=BD，
过点C作CE⊥AB，垂足为E，则
S△ADC=
×AD×CE=4，
S△CDB=×BD×CE=×AD×CE=4．
故答案为：4．
点评：本题考查了三角形的面积的求解，利用三角形的面积公式推出等底同高的两个三角形的面积相等，熟记此规律对今后的学习大有帮助．
分析：根据三角形的中线定义得点D是AB的中点，所以AD=BD，再根据两三角形的高是同一条高，可得两三角形的面积相等．
解答：
解：∵CD是△ABC的中线，∴D是AB的中点，
∴AD=BD，
过点C作CE⊥AB，垂足为E，则
S△ADC=
×AD×CE=4，S△CDB=
×BD×CE=×AD×CE=4．故答案为：4．
点评：本题考查了三角形的面积的求解，利用三角形的面积公式推出等底同高的两个三角形的面积相等，熟记此规律对今后的学习大有帮助．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
2、如图所示，若DE⊥AB，DF⊥AC，则对于∠1和∠2的大小关系下列说法正确的是（ ）
对上述命题证明如下：
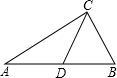如图所示，若CD是△ABC的中线，S△ADC=4，则S△CDB=
如图所示，点C是线段AB上的点，点D是线段BC的中点，若AB=12，AC=8，求CD的值．