题目内容
6.已知关于x的方程(m-1)xn-1-3=0是一元一次方程.(1)则m,n应满足的条件为m≠1,n=2;
(2)若此方程的根为整数,求整数m的值.
分析 (1)根据一元一次方程的定义可得m-1≠0,n-1=1,再解即可;
(2)首先移项得(m-1)x=3,然后根据方程的根为整数可得m-1=1或-1或3或-3,再解即可.
解答 解:(1)由题意得:m-1≠0,n-1=1,
解得:m≠1,n=2,
故答案为:≠1;=2;
(2)(m-1)x-3=0,
(m-1)x=3,
∵此方程的根为整数,
∴m-1=1或-1或3或-3,
m=2,0,4,-2.
点评 此题主要考查了一元一次方程的定义,以及方程的解,关键是掌握只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程.

练习册系列答案
相关题目
14.若式子$\frac{1-x}{2}$与1-$\frac{x+1}{3}$的值相等,则x=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
1. 如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
 如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
如图,在四边形ABCD中,点E,F,G,H分别是AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )| A. | AB⊥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
11.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
18.下列四组等式变形中,正确的是( )
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | D. | 由5x=7.得x=$\frac{5}{7}$ |
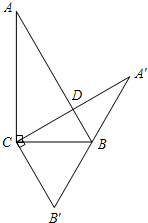 在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.