题目内容
7.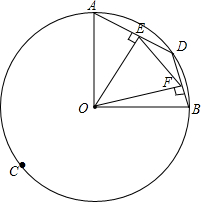 已知:如图,在⊙O中,OA、OB为⊙O的半径,且OA⊥OB,点D为$\widehat{AB}$(不与A、B重合)上一动点,过点O作OE⊥AD于点E,过点O作OF⊥DB于点F.
已知:如图,在⊙O中,OA、OB为⊙O的半径,且OA⊥OB,点D为$\widehat{AB}$(不与A、B重合)上一动点,过点O作OE⊥AD于点E,过点O作OF⊥DB于点F.(1)求$\widehat{ACB}$的度数以及∠ADB的度数;
(2)随着点D在$\widehat{AB}$上的运动,EF的长度会发生变化吗?请说明理由;
(3)若已知弦AD=4$\sqrt{2}$,弦BD=4,求⊙O的半径.
分析 (1)由∠AOB=90°,根据圆心角、弧、弦的关系即可求得$\widehat{ACB}$的度数以及∠ADB的度数;
(2)连接AB,根据垂径定理得出EF是△ABD的中位线,根据三角形的中位线定理即可证得结论;
(3)作BG⊥AD,交AD的延长线于G,得出△BDG是等腰直角三角形,根据勾股定理即可求得BG和DG,进而得出AG的长,根据勾股定理求得AB的平方,然后再通过勾股定理即可求得圆的半径.
解答  解:(1)∵OA⊥OB,
解:(1)∵OA⊥OB,
∴∠AOB=90°,
∴$\widehat{ACB}$的度数为270°,
∴∠ADB=135°,;
(2)EF的长度不会发生变化,
理由:如图,连接AB,
∵OE⊥AD,OF⊥DB,
∴AE=DE,DF=BF,
∴EF=$\frac{1}{2}$AB,
因为AB是定值,所以EF的长度不会发生变化;
(3)如图,作BG⊥AD,交AD的延长线于G,
∵∠ADB=135°,
∴∠BDG=45°,
∴△BDG是等腰直角三角形,
∴BG=DG,
∵BD2=BG2+DG2,BD=4,
∴BG=DG=$\sqrt{\frac{B{D}^{2}}{2}}$=2$\sqrt{2}$,
∴AG=D+DG=4$\sqrt{2}$+2$\sqrt{2}$=6$\sqrt{2}$,
在RT△ABG中,AB2=AG2+BG2=(6$\sqrt{2}$)2+(2$\sqrt{2}$)2=80,
在RT△AOB中,AB2=OA2+OB2,
∵OA=OB,
∴2OA2=80,
∴OA=2$\sqrt{10}$.
∴⊙O的半径为2$\sqrt{10}$.
点评 本题考查了垂径定理,圆心角、弧、弦的关系,三角形的中位线定理以及勾股定理,作出辅助线构建等腰直角三角形是解题的关键.

练习册系列答案
相关题目
15.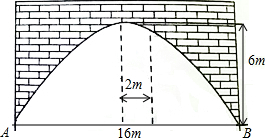 如图,有一个抛物线型拱桥,桥洞离水面的最大高度为6m,跨度为16m,请建立适当的直角坐标系.
如图,有一个抛物线型拱桥,桥洞离水面的最大高度为6m,跨度为16m,请建立适当的直角坐标系.
(1)求这条抛物线所对应的函数表达式;
(2)在这条抛物线的对称轴右边2m处,桥洞离水面的高度是多少?
 如图,有一个抛物线型拱桥,桥洞离水面的最大高度为6m,跨度为16m,请建立适当的直角坐标系.
如图,有一个抛物线型拱桥,桥洞离水面的最大高度为6m,跨度为16m,请建立适当的直角坐标系. (1)求这条抛物线所对应的函数表达式;
(2)在这条抛物线的对称轴右边2m处,桥洞离水面的高度是多少?
12.已知线段AB,点C是它的黄金分割点(AC>BC).设以AC为边的正方形的面积为S1,以AB、CB分别为长和宽的矩形的面积为S2,则S1与S2关系正确的是( )
| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
 如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.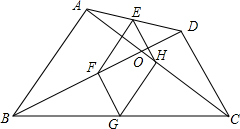 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.