题目内容
要建造一个面积为35m2的长方形仓库,仓库的一边靠墙(墙长大于17m),其余三边的总长度为17m,问所建长方形仓库的长和宽各是多少?
考点:一元二次方程的应用
专题:几何图形问题
分析:设垂直墙的篱笆的长为x,那么余下的篱笆长为(17-2x),x和(17-2x)就是养鸡场的长或宽.然后用面积做等量关系可列方程求解.
解答: 解:设垂直墙的仓库的长是x米.由题意,得
解:设垂直墙的仓库的长是x米.由题意,得
(17-2x)x=35,
解得:x=3.5或x=5,
∵0<17-2x<17,
0<x≤8.5,
x=3.5或x=5都符合题意,
当x=3.5时,17-2x=10.
当x=5时,17-2x=7.
答:仓库的长是10m,宽是3.5m,或仓库的长是7m,宽是5m.
 解:设垂直墙的仓库的长是x米.由题意,得
解:设垂直墙的仓库的长是x米.由题意,得(17-2x)x=35,
解得:x=3.5或x=5,
∵0<17-2x<17,
0<x≤8.5,
x=3.5或x=5都符合题意,
当x=3.5时,17-2x=10.
当x=5时,17-2x=7.
答:仓库的长是10m,宽是3.5m,或仓库的长是7m,宽是5m.
点评:考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题是用17m的篱笆围成三个边.

练习册系列答案
相关题目
若双曲线y=-
经过点A(-2,n),则n的值为( )
| 6 |
| x |
A、
| ||
| B、3 | ||
C、±
| ||
| D、±3 |
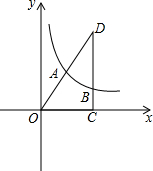 已知:如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
已知:如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A. 如图,一个棱长为10cm的正方体,在它的一个角上挖掉一个棱长是2cm的正方体,求出剩余部分的表面积和体积.
如图,一个棱长为10cm的正方体,在它的一个角上挖掉一个棱长是2cm的正方体,求出剩余部分的表面积和体积.