Question

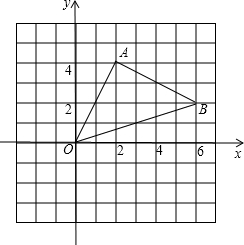如图，△AOB中，A，B两点的坐标分别为（2，4）、（6，2），
求：△AOB的面积．
（△AOB的面积可以看作一个长方形的面积减去一些小三角形的面积）

Answer 1

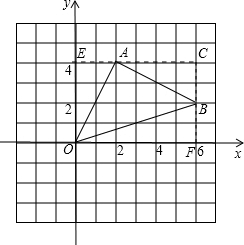解：过点A、B分别作x轴、y轴的垂线CE、CF交点为C，垂足分别为E、F
∵A（2，4）、B（6，2）
∴OE=AC=4，EA=CB=BF=2，OF=6，
∴S_ECFO=6×4=24 …（2分）
S_△AOE=×4×2=4 …（4分）
S_△ACB=×4×2=4 …（6分）
S_△BOF=×6×2=6 …（8分）
∴S_△AOB=S_ECFO-S_△AOE-S_△ACB-S_△BOF
=24-4-4-6
=10 …（10分）
∴△AOB的面积是10．
分析：作辅助线（过点A、B分别作x轴、y轴的垂线CE、CF交点为C，垂足分别为E、F）构建矩形ECFO．根据矩形的四个角都是直角的性质求得矩形的面积、矩形ECFO中△AEO、△ABC、△BFO的面积，从而求得S_△AOB=S_ECFO-S_△AOE-S_△ACB-S_△BOF．
点评：本题考查了三角形的面积、坐标与图形的性质．解答该题时，利用点的坐标求得相关线段的长度，然后根据图形的面积公式求解．