题目内容
矩形ABCD的两条对角线相交于点O，∠AOB=60°，则对角线AC与边BC所成的角是
- A.15°
- B.30°
- C.45°
- D.60°
B
分析：根据矩形的对角线的性质，结合等腰三角形的性质求解．
解答：根据矩形的对角线相等且互相平分得到：OB=OC．
则∠ACB=∠OBC．
∵∠AOB=∠ACB+∠OBC
∴∠ACB=30°．
故选B．
点评：本题主要考查了矩形的对角线相等且平分．即对角线把矩形分成了四个等腰三角形．
分析：根据矩形的对角线的性质，结合等腰三角形的性质求解．
解答：根据矩形的对角线相等且互相平分得到：OB=OC．
则∠ACB=∠OBC．
∵∠AOB=∠ACB+∠OBC
∴∠ACB=30°．
故选B．
点评：本题主要考查了矩形的对角线相等且平分．即对角线把矩形分成了四个等腰三角形．
练习册系列答案
相关题目
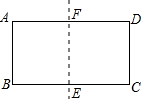如图所示，将矩形ABCD沿两条较长边的中点的连线对折，如果矩形BEFA与矩形ABCD相似，那么AB：AD等于（ ）A、
| ||
B、1：
| ||
C、
| ||
D、1：
|
请将下面证明中每一步的理由填在括号内：
