题目内容
 请将下面证明中每一步的理由填在括号内:
请将下面证明中每一步的理由填在括号内:如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,求矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC=BD,且OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
矩形的对角线相等且互相平分
矩形的对角线相等且互相平分
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD=
| 180°-120° |
| 2 |
等边对等角
等边对等角
∵∠DAB=90°
矩形的四个角都是直角
矩形的四个角都是直角
∴BD=2AB=2×2.5=5
直角三角形30°角所对的直角边等于斜边的一半
直角三角形30°角所对的直角边等于斜边的一半
.分析:根据矩形的性质、等腰三角形的判定以及含30度角的直角三角形的性质填空即可.
解答:解:∵四边形ABCD是矩形,
∴AC=BD,且OA=OC=
AC,OB=OD=
BD(矩形的对角线相等且互相平分),
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD=
=30°(等边对等角),
∵∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×2.5=5(直角三角形30°角所对的直角边等于斜边的一半),
故答案为:矩形的对角线相等且互相平分,等边对等角,矩形的四个角都是直角,直角三角形30°角所对的直角边等于斜边的一半;
∴AC=BD,且OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OD.
∵∠AOD=120°,
∴∠ODA=∠OAD=
| 180°-120° |
| 2 |
∵∠DAB=90°(矩形的四个角都是直角),
∴BD=2AB=2×2.5=5(直角三角形30°角所对的直角边等于斜边的一半),
故答案为:矩形的对角线相等且互相平分,等边对等角,矩形的四个角都是直角,直角三角形30°角所对的直角边等于斜边的一半;
点评:此题考查了矩形的性质、等腰三角形的性质、含30度角的直角三角形的性质、此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 请将下面证明中的每一步理由填在括号内:
请将下面证明中的每一步理由填在括号内: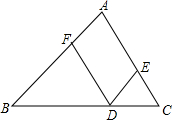 请将下面证明中的每一步理由填在括号内:
请将下面证明中的每一步理由填在括号内:
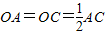 ,
,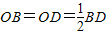 ______
______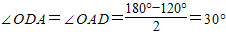 .______
.______