Question

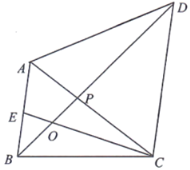
【题目】如图，四边形ABCD中，,,,对角线BD平分交AC于点P.CE是的角平分线,交BD于点O.

（1）请求出的度数;

（2）试用等式表示线段BE、BC、CP之间的数量关系，并说明理由;

Answer 1

【答案】（1）；（2）BE+CP=BC，理由见解析．

【解析】

（1）先证得为等边三角形，再利用平行线的性质可求得结论；

（2）由BP、CE是△ABC的两条角平分线，结合BE=BM，依据“SAS”即可证得△BEO≌△BMO；利用三角形内角和求出∠BOC=120°，利用角平分线得出∠BOE=∠BOM=60，求出∠BOM，即可判断出∠COM=∠COP，即可判断出△OCM≌△OCP，即可得出结论；

（1）∵，，

∴为等边三角形，

∴∠ACD=，

∵，

∴∠BAC=∠ACD=；

（2）BE+CP=BC，理由如下：

在BC上取一点M，使BM=BE，连接OM，如图所示：

∵BP、CE是△ABC的两条角平分线，

∴∠OBE=∠OBM=∠ABC，

在△BEO和△BMO中，，

∴△BEO△BMO(SAS)，

∴∠BOE=∠BOM=60，

∵BP、CE是△ABC的两条角平分线，
∴∠OBC+∠OCB=

在△ABC中，∠BAC+∠ABC+∠ACB=180，
∵∠BAC =60，
∴∠ABC+∠ACB=180-∠A=180-60=120，
∴∠BOC=180-(∠OBC+∠OCB)=180=180-×120=120，

∴∠BOE=60，

∴∠COP=∠BOE=60
∵△BEO≌△BMO，
∴∠BOE=∠BOM=60，
∴∠COM=∠BOC-∠BOM=120-60=60，
∴∠COM=∠COP=60，
∵CE是∠ACB的平分线，
∴∠OCM=∠OCP，
在△OCM和△OCP中，

∴△OCM≌△OCP（ASA），
∴CM=CP，
∴BC=CM+BM=CP+BE，
∴BE+CP=BC．