题目内容
5.解方程组:$\left\{\begin{array}{l}{\sqrt{2}x+\sqrt{3}y=3\sqrt{2}}\\{\sqrt{3}x-\sqrt{2}y=2\sqrt{3}}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{\sqrt{2}x+\sqrt{3}y=3\sqrt{2}①}\\{\sqrt{3}x-\sqrt{2}y=2\sqrt{3}②}\end{array}\right.$,
①×$\sqrt{2}$+②×$\sqrt{3}$得:5x=12,即x=$\frac{12}{5}$,
把x=$\frac{12}{5}$代入①得:y=$\frac{\sqrt{6}}{5}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=\frac{\sqrt{6}}{5}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,该几何体的俯视图是( )
如图,该几何体的俯视图是( )
 如图,该几何体的俯视图是( )
如图,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
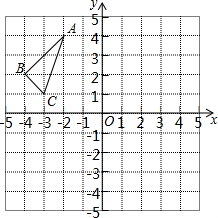 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度. 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=$\frac{9}{10}$.其中正确的有①③(填写序号).
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=$\frac{9}{10}$.其中正确的有①③(填写序号).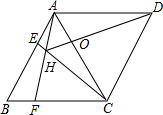 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( ) ,当x=1时,请你选择一个恰当的y值代入求值.
,当x=1时,请你选择一个恰当的y值代入求值.