��Ŀ����
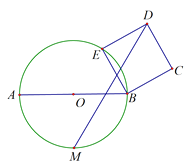
����Ŀ����������![]() ��x��Ľ���ֱ�ΪA��B����A�ڵ�B����ࣩ������ΪC����a��b��c����
��x��Ľ���ֱ�ΪA��B����A�ڵ�B����ࣩ������ΪC����a��b��c����![]() ����Ƹ�������Ϊ������������������a��b��c����
����Ƹ�������Ϊ������������������a��b��c����![]() ����Ƹ�������Ϊ�����������������ر�أ���ij��������������������������������������������Ƹ�������Ϊ���Գ�����������
����Ƹ�������Ϊ�����������������ر�أ���ij��������������������������������������������Ƹ�������Ϊ���Գ�����������
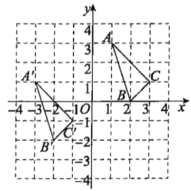
��1�����������������ؾ���x���ϵĶ���___________�����������������ؾ���x���ϵĶ���___________��
��2����������![]() �����Գ���������������ABC�ǵȱ������Σ���������߶�Ӧ�ĺ�������ʽ��
�����Գ���������������ABC�ǵȱ������Σ���������߶�Ӧ�ĺ�������ʽ��
��3����������![]() ��������������������������߽�y���ڵ�D����BCD�����ΪS����S��b֮��ĺ�����ϵʽ��
��������������������������߽�y���ڵ�D����BCD�����ΪS����S��b֮��ĺ�����ϵʽ��
��4������������������![]() (b>0)��x��Ľ���ֱ�Ϊ
(b>0)��x��Ľ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����ࣩ������ΪM����������������
����ࣩ������ΪM����������������![]() (b>0)��x��Ľ���ֱ�Ϊ
(b>0)��x��Ľ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����ࣩ������ΪN������������������Ӧ�ĺ�������ʽ�У���ͬʱ����y��x�����������ʱ������x��ֵ��x��������Ӧ�ĵ�ǡ�����߶�
����ࣩ������ΪN������������������Ӧ�ĺ�������ʽ�У���ͬʱ����y��x�����������ʱ������x��ֵ��x��������Ӧ�ĵ�ǡ�����߶�![]()
![]() �������˵㣩ʱ��ֱ��д����ʱ��M��N��
�������˵㣩ʱ��ֱ��д����ʱ��M��N��![]() ��
��![]() Ϊ������ı��ε������
Ϊ������ı��ε������
���𰸡���1����1��0������-1��0������2��![]() ����3����
����3����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����4��8��
����4��8��
����������1����������������a��b��c����![]() ������x=1ʱ��y=a+b+c=0,���㣨1,0������������������a��b��c����
������x=1ʱ��y=a+b+c=0,���㣨1,0������������������a��b��c����![]() ������x=-1ʱ��y=a-b+c=0,���㣨-1,0����
������x=-1ʱ��y=a-b+c=0,���㣨-1,0����
��2���������Գ����������Ķ��壬��֪�����߾�����1,0������-1,0����������ABC�ǵȱ������Σ��ó�c=![]() ��c=-
��c=-![]() ���Ӷ�����������߶�Ӧ�Ľ���ʽ��
���Ӷ�����������߶�Ӧ�Ľ���ʽ��
��3��������![]() ������������������ �����߾�����1,0���������1+b+c=0����c=-b-1����ʾ��C��
������������������ �����߾�����1,0���������1+b+c=0����c=-b-1����ʾ��C��![]() ��
��![]() ����D��0��-b-1����Ȼ����������д��S���ɣ�
����D��0��-b-1����Ȼ����������д��S���ɣ�
��4����������y��x�����������ʱ������x��ֵ��x��������Ӧ�ĵ�ǡ�����߶�![]()
![]() �������˵㣩��֪����������������
�������˵㣩��֪����������������![]() (b>0)�ĶԳ�����x=-1����������������
(b>0)�ĶԳ�����x=-1����������������![]() (b>0) �ĶԳ�����x=1������������������������������������Ķ�����⼴��.
(b>0) �ĶԳ�����x=1������������������������������������Ķ�����⼴��.
��1����������������a��b��c����![]() ������x=1ʱ��y=a+b+c=0,���㣨1,0������������������a��b��c����
������x=1ʱ��y=a+b+c=0,���㣨1,0������������������a��b��c����![]() ������x=-1ʱ��y=a-b+c=0,���㣨-1,0����
������x=-1ʱ��y=a-b+c=0,���㣨-1,0����
��2����������![]() �����Գ�����������
�����Գ�����������
�������߾����㣨1��0������-1��0����
��![]() ���
���![]()
�ߡ�ABC�ǵȱ������Σ�
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�������߶�Ӧ�ĺ�������ʽΪ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�������߶�Ӧ�ĺ�������ʽΪ![]() ��
��
��3����������![]() ������������������
������������������
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ߵ�CΪ�����ߵĶ��㣬��DΪ�����ߺ�y��Ľ��㣬
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��/p>
ʱ��/p>
![]()
��4��������ã���������������![]() (b>0)�ĶԳ�����x=-1����������������
(b>0)�ĶԳ�����x=-1����������������![]() (b>0) �ĶԳ�����x=1��
(b>0) �ĶԳ�����x=1��
��![]() ��
��
��b=2.
��![]() ������������������
������������������
��1+b+m=0,
��m=-b-1=-3,
��M�������![]() ��
��
��A2M=4.
ͬ������B1N=4��
��A2M=B1N��
���ı���A2MB1N��ƽ���ı�����
��S�ı���A2MB1N=2��4=8��


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�����Ŀ����ͼ��������ABCD�ڲ������ɸ��㣬����Щ���Լ�������ABCD�Ķ���A��B��C��D��ԭ�����ηָ��һЩ�����Σ�����ص�����
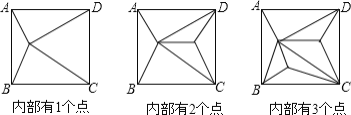
��1��������
������ABCD�ڵ�ĸ��� | 1 | 2 | 3 | 4 | �� | n |
�ָ�ɵ������εĸ��� | 4 | 6 | �� �� | �� �� | �� | �� �� |
��2��ԭ�������ָܷ��2019�������Σ����ܣ����ʱ������ABCD�ڲ��ж��ٸ��㣿�����ܣ���˵�����ɣ�