题目内容
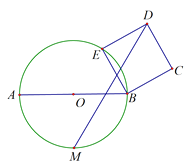
【题目】如图：已知⊙O的半径为6，E是⊙O上一个动点，以BE为边按顺时针方向做正方形BEDC，M是弧AB的中点，当E在圆上移动时，MD的最小值是_______
【答案】
【解析】连接CE并延长交⊙O于点T，则∠TED=∠TEB，由TE=TE，ED=EB，得到△TED≌△TEB，故TD=TB，从而得到点D的运动轨迹就是以T为圆心，TD为半径的圆．连接TO，可得出TB=TD=
．连接OM交⊙T于点D′，此时MD′最短，即可得出结论．
连接CE并延长交⊙O于点T，则∠TED=∠TEB=180°-45°=135°．
∵TE=TE，∠TED=∠TEB，ED=EB，∴△TED≌△TEB，∴TD=TB，∴点D的运动轨迹就是以T为圆心，TD为半径的圆．
连接TO，则∠TOB=90°，∴TO=OB=6，∴TB=TD=．
连接OM交⊙T于点D′，此时MD′最短，∴MD的最小值为MD′=TM－TD′=
=
．故答案为：．
练习册系列答案
全能练考卷系列答案
相关题目
