题目内容
已知，如图△ABC是等边三角形，将一块含30°角的直角三角板DEF如图放置，让△ABC在BC所在的直线l上向左平移．当点B与点E重合时，点A恰好落在三角板的斜边DF上的M点，点C在N点位置上（假定AB、AC与三角板斜边的交点为G、H）
问：（1）在△ABC平移过程中，通过测量CH、CF的长度，猜想CH、CF满足的数量关系；
（2）在△ABC平移过程中，通过测量BE、AH的长度，猜想BE．AH满足的数量关系；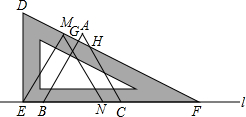
（3）证明（2）中你的猜想．（证明不得含有图中未标示的字母）
解：（1）CH=CF …
（2）BE=AH…
（3）证明：连接AM，由平移的性质可知：AM=BE，AM∥CN
则∠AMF=∠DFE=30°
∵△ABC等边三角形，
∴∠ACB=60°
又∵∠ACB=∠DFE+∠CHF=60°
∴∠CHF=30°
∵∠CHF=∠AHM=30°
∴∠AMF=∠AHM…
∴AM=AH
∴BE=AH…
（注：其它方法也可求出，可相应给分）
分析：由题意易得四边形MEBA为平行四边形，可得BE=MA，AM∥EF，那么∠AMH=∠F=30°，而∠AHM=FMN=30°，可得∠AHM=∠NMF，那么MA=AH，也就得到EB=AH．
点评：本题主要运用了平移的性质和特殊三角形的角进行求解．找相等线段，应把已知线段进行转移，利用第三条线段求解．
（2）BE=AH…
（3）证明：连接AM，由平移的性质可知：AM=BE，AM∥CN
则∠AMF=∠DFE=30°
∵△ABC等边三角形，
∴∠ACB=60°
又∵∠ACB=∠DFE+∠CHF=60°
∴∠CHF=30°
∵∠CHF=∠AHM=30°
∴∠AMF=∠AHM…
∴AM=AH
∴BE=AH…
（注：其它方法也可求出，可相应给分）
分析：由题意易得四边形MEBA为平行四边形，可得BE=MA，AM∥EF，那么∠AMH=∠F=30°，而∠AHM=FMN=30°，可得∠AHM=∠NMF，那么MA=AH，也就得到EB=AH．
点评：本题主要运用了平移的性质和特殊三角形的角进行求解．找相等线段，应把已知线段进行转移，利用第三条线段求解．
练习册系列答案
阅读快车系列答案
相关题目
6、已知：如图△ABC是等边三角形，过AB边上的点D作DG∥BC，交AC于点G，在GD的延长线上取点E，使DE=DB，连接AE、CD．
已知：如图△ABC是边长为4的等边三角形，点P、Q分别从A、C两点同时出发，速度为每秒1个单位长度，B与原点重合，PQ交AC于D．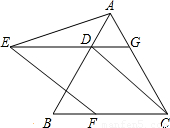
上取点E，使DE=DB，连接AE、CD．