题目内容
 已知:如图△ABC是边长为4的等边三角形,点P、Q分别从A、C两点同时出发,速度为每秒1个单位长度,B与原点重合,PQ交AC于D.
已知:如图△ABC是边长为4的等边三角形,点P、Q分别从A、C两点同时出发,速度为每秒1个单位长度,B与原点重合,PQ交AC于D.(1)写出点A的坐标
(2,2
)
| 3 |
(2,2
)
;| 3 |
(2)当△DCQ为等腰三角形时,求t的值;
(3)若△PCQ的面积为S,P、Q运动的时间为t秒,求S与t的函数关系式,并求S的最大值.
分析:(1)过点A作AE⊥OC于点E,根据等边三角形的性质,可得出OE、AE的长度,继而得出点A的坐标;
(2)△DCQ为等腰三角形,则可得∠PQO=30°,则△POQ是含30°角的直角三角形,根据OQ=2OP,可得出t的值;
(3)过点P作PF⊥OC于点F,先表示出OP,在Rt△OPF中表示出PF,继而可表示出△PCQ的面积,利用配方法求最值即可.
(2)△DCQ为等腰三角形,则可得∠PQO=30°,则△POQ是含30°角的直角三角形,根据OQ=2OP,可得出t的值;
(3)过点P作PF⊥OC于点F,先表示出OP,在Rt△OPF中表示出PF,继而可表示出△PCQ的面积,利用配方法求最值即可.
解答:解:(1)过点A作AE⊥OC于点E,
∵△ABC是等边三角形,
∴OE=
OA=2,AE=
OE=2
,
∴点A的坐标为(2,2
);
 (2)∵△CDQ为等腰三角形,∠DCQ=120°,
(2)∵△CDQ为等腰三角形,∠DCQ=120°,
∴∠CDQ=∠CQD=30°,
又∵∠AOC=60°,
∴△OPQ为直角三角形,
∴OQ=2OP,即4+t=2(4-t),
解得:t=
;
(3)过点P作PF⊥OC于点F,
∵OP=4-t,∠OPE=30°,
∴OF=
,PF=
OF=
,
∴S△PCQ=
CQ×PF=
×t×
=-
t2+
t=-
(t-2)2+
,
∴当t=2时,△PCQ的面积最大,S的最大值为
.
∵△ABC是等边三角形,
∴OE=
| 1 |
| 2 |
| 3 |
| 3 |
∴点A的坐标为(2,2
| 3 |
 (2)∵△CDQ为等腰三角形,∠DCQ=120°,
(2)∵△CDQ为等腰三角形,∠DCQ=120°,∴∠CDQ=∠CQD=30°,
又∵∠AOC=60°,
∴△OPQ为直角三角形,
∴OQ=2OP,即4+t=2(4-t),
解得:t=
| 4 |
| 3 |
(3)过点P作PF⊥OC于点F,
∵OP=4-t,∠OPE=30°,
∴OF=
| 4-t |
| 2 |
| 3 |
4
| ||||
| 2 |
∴S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||||
| 2 |
| ||
| 4 |
| 3 |
| ||
| 4 |
| 3 |
∴当t=2时,△PCQ的面积最大,S的最大值为
| 3 |
点评:本题考查了二次函数的综合,涉及了动点问题、等边三角形的性质、含30°角的直角三角形的性质及配方法求二次函数最值的知识,解答本题关键是基本知识的融会贯通.

练习册系列答案
相关题目
 6、已知:如图△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD.
6、已知:如图△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD.
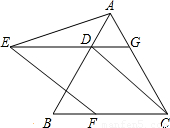 上取点E,使DE=DB,连接AE、CD.
上取点E,使DE=DB,连接AE、CD.