题目内容
 如图,Rt△ABC的顶点坐标分别为A(0,
如图,Rt△ABC的顶点坐标分别为A(0,| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
(1)求该抛物线的解析式.
(2)将△ABC沿AC折叠后得到点B的对应点B',求证:四边形AOCB'是矩形,并判断点B'是否在(1)的抛物线上.
(3)延长BA交抛物线于点E,在线段BE上取一点P,过点P作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)设抛物线解析式,因点B在抛物线上面,代入求出抛物线解析式;
(2)△ABC沿AC折叠,要用到点的对称,得到B′的坐标然后验证是否在抛物线上;
(3)假设存在,设直线BA的解析式,根据B、A坐标解出直线BA的解析式,用m表示出P点坐标,因为PF=AD可以得到P点坐标.
(2)△ABC沿AC折叠,要用到点的对称,得到B′的坐标然后验证是否在抛物线上;
(3)假设存在,设直线BA的解析式,根据B、A坐标解出直线BA的解析式,用m表示出P点坐标,因为PF=AD可以得到P点坐标.
解答: 解:(1)设抛物线的解析式为y=ax2+
解:(1)设抛物线的解析式为y=ax2+
,(1分)
∵B(-
,
)在抛物线上,
∴把B(-
,
)代入y=ax2+
得a=
.(3分)
∴抛物线解析式为y=
x2+
.(5分)
(2)∵点B(-
,
),A(0,
),
∴CB=
=
,
∴CB'=CB=OA.(6分)
又CA=
=2
∴AB=
=1
∴AB'=AB=OC.(7分)
∴四边形AOCB'是矩形.(8分)
∵CB'=
,OC=1,
∴B'点的坐标为(1,
).(9分)
∵当x=1时,代入y=
x2+
得y=
,
∴B'(1,
)在抛物线上.(10分)
(3)存在.(11分)
理由是:设BA的解析式为y=kx+b,
∴
∴
∵P,F分别在直线BA和抛物线上,且PF∥AD,
∴设P(m,
m+
),F(m,
m2+
)
PF=(
m+
)-(
m2+
),AD=
-
=
如果PF=AD,则有
=(
m+
)-(
m2+
)=
解得m1=0(不符合题意舍去),m2=
.
∴当m=
时,PF=AD,
存在四边形ADFP是平行四边形.(13分)
当m=
时,
m+
=
,
∴P点的坐标是(
,
).(14分)
 解:(1)设抛物线的解析式为y=ax2+
解:(1)设抛物线的解析式为y=ax2+
| ||
| 3 |
∵B(-
| 1 |
| 2 |
| ||
| 2 |
∴把B(-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
得a=
| 2 |
| 3 |
| 3 |
∴抛物线解析式为y=
| 2 |
| 3 |
| 3 |
| ||
| 3 |
(2)∵点B(-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CB=
(
|
| 3 |
∴CB'=CB=OA.(6分)
又CA=
12+(
|
∴AB=
| AC2-BC2 |
∴AB'=AB=OC.(7分)
∴四边形AOCB'是矩形.(8分)
∵CB'=
| 3 |
∴B'点的坐标为(1,
| 3 |
∵当x=1时,代入y=
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
∴B'(1,
| 3 |
(3)存在.(11分)
理由是:设BA的解析式为y=kx+b,
∴
|
∴
|
∵P,F分别在直线BA和抛物线上,且PF∥AD,
∴设P(m,
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
PF=(
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 3 |
如果PF=AD,则有
=(
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 3 |
解得m1=0(不符合题意舍去),m2=
| 3 |
| 2 |
∴当m=
| 3 |
| 2 |
存在四边形ADFP是平行四边形.(13分)
当m=
| 3 |
| 2 |
| 3 |
| 3 |
5
| ||
| 2 |
∴P点的坐标是(
| 3 |
| 2 |
5
| ||
| 2 |
点评:考查待定系数求抛物线解析式,折叠图形的对称问题,辅助线的作法也很独特,考查的知识点很全面,是一道综合性题型.

练习册系列答案
相关题目
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线 如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是
如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是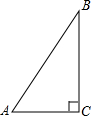 如图,Rt△ABC的斜边AB=10cm,
如图,Rt△ABC的斜边AB=10cm,
 如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.
如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.