题目内容
6. 如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.
如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.(1)求两灯杆的距离DB;
(2)某县在一条长760m的大街P-K-Q上安装12根灯杆(含两端),其中PK为休闲街,按(1)中的灯杆距离安装灯杆,KQ为购物街,灯杆距离比(1)中的少35m,求休闲街和购物街分别长多少米.
(参考数据:tan78.69°≈5.00,tan11.31°≈0.20,cos78.69°≈0.20,cos11.31°≈0.98,可使用科学计算器)
分析 (1)由∠EHG=∠NEH=11.31°,分别在Rt△ABH与Rt△EFH中,利用三角函数的知识即可求得BH与FH的长,继而求得答案;
(2)首先设休闲街长x米,则购物街长为(760-x)米,根据题意列出方程,解方程求得答案.
解答 解:解:(1)∵MN∥BD,
∴∠EHG=∠NEH=11.31°,
∴在Rt△ABH中,BH=$\frac{AB}{tan11.31°}$≈$\frac{10}{0.20}$=50(米),
在Rt△EFH中,FH=$\frac{EF}{tan11.31°}$≈$\frac{1.5}{0.20}$=7.5(米),
∴BF=BH-FH=42.5(米),
∴DB=2BF=85(米);
答:两灯秆的距离DB为85米;
(2)设休闲街长x米,则购物街长为(760-x)米,
$\frac{x}{85}$+$\frac{760-x}{85-35}$=12-1,
解得:x=510,
760-510=250(米),
答:休闲街和购物街分别长510米,250米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题以及一元一次方程的应用,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.已知am=2,an=$\frac{1}{2}$,a2m+3n的值为( )
| A. | 6 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{11}{2}$ |
11.把分式方程$\frac{1}{x-2}$-$\frac{1-x}{2-x}$=1化为整式方程正确的是( )
| A. | 1-(1-x)=1 | B. | 1+(1-x)=1 | C. | 1-(1-x)=x-2 | D. | 1+(1-x)=x-2 |
15.200粒大米重约4克,如果每人每天浪费1粒米,那么约458万人口的漳州市每天浪费大米用科学记数法表示约为( )
| A. | 9.16×103克 | B. | 9.16×104克 | C. | 9,16×105克 | D. | 0.916×105克 |
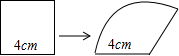 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2. 一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度.
一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度.